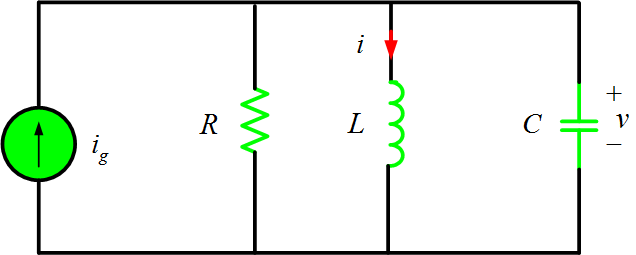
When resistance, inductance, and capacitance are connected in parallel, the circuit is said to be RLC Parallel circuit. In the parallel RLC circuit shown in the figure below, the supply voltage is common to all components.
One of the most important second-order circuits is the parallel RLC circuit of figure 1 (a).
Fig.1 (a): Parallel RLC Circuit
We shall assume that at t=0 there is an initial inductor current,
$\begin{matrix} i(0)={{I}_{o}} & \cdots & (1) \\\end{matrix}$
And an initial capacitor voltage,
$\begin{matrix} v(0)={{V}_{o}} & \cdots & (2) \\\end{matrix}$
And analyze the circuit by finding v for t>0.
The single nodal equation that is necessary is given by
$\begin{matrix} \frac{v}{R}+\frac{v}{R}\int\limits_{0}^{t}{v}dt+{{I}_{o}}+C\frac{dv}{dt}={{i}_{g}} & \cdots & (3) \\\end{matrix}$
Which is an integral-differential equation that becomes, upon differentiation,
$\begin{matrix} C\frac{{{d}^{2}}v}{d{{t}^{2}}}+\frac{1}{R}\frac{dv}{dt}+\frac{1}{L}v=\frac{d{{i}_{g}}}{dt} & {} & {} \\\end{matrix}$
To find the natural response we make the right member zero, resulting in
$\begin{matrix} C\frac{{{d}^{2}}v}{d{{t}^{2}}}+\frac{1}{R}\frac{dv}{dt}+\frac{1}{L}v=0 & \cdots & (4) \\\end{matrix}$
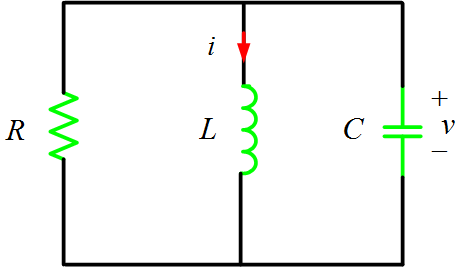
Fig.1 (b): Parallel RLC Circuit without Source
- You May Also Read: Series RLC Circuit Analysis
This result follows also from killing the current source, as in figure 1 (b), and writing the nodal equation. From (4) the characteristic equation is
$C{{s}^{2}}+\frac{1}{R}s+\frac{1}{L}=0$
From which the natural frequencies are
[stextbox id=”info”]$\begin{align} & \begin{matrix} {{s}_{1,2}}=-\frac{1}{2RC}\pm \sqrt{{{\left( \frac{1}{2RC} \right)}^{2}}-\frac{1}{LC}} & \cdots & (5) \\\end{matrix} \\ & \\\end{align}$[/stextbox]
As in the general second order case, there are three types of responses, depending on the nature of the discriminant, ${{\left( {}^{1}/{}_{2RC} \right)}^{2}}-\left( {}^{1}/{}_{LC} \right)$ , in (5). We shall now look briefly at these three cases. For simplicity we will take ig=0 and consider the source free case of figure 1 (b). The forced response is then zero and the natural response is the complete response.
Overdamped case
If the discriminant is positive, that is:
${{\left( {}^{1}/{}_{2RC} \right)}^{2}}-\left( {}^{1}/{}_{LC} \right)>0$
Or equivalently,
$\begin{matrix} L>4{{R}^{2}}C & \cdots & (6) \\\end{matrix}$
Then the natural frequencies of (5) are real and distinct negative numbers, and we have the overdamped case,
[stextbox id=”info” caption=”Over-damped Case”]\[\begin{matrix} v={{A}_{1}}{{e}^{{{s}_{1}}t}}+{{A}_{2}}{{e}^{{{s}_{2}}t}} & \cdots & (7) \\\end{matrix}\][/stextbox]
From the initial conditions and (3) evaluated at t=0+, we obtain
$\begin{matrix} \frac{dv({{0}^{+}})}{dt}=-\frac{{{V}_{o}}+R{{I}_{o}}}{RC} & \cdots & (8) \\\end{matrix}$
Which together with (2) can be used to determine the arbitrary constants.
As an example, suppose R=1Ω, L=4/3H, C=1/4F, Vo=2V, and Io=-3A. Then by (5) we have${{s}_{1,2}}=-1,-3$, and hence
\[\begin{matrix} v={{A}_{1}}{{e}^{-t}}+{{A}_{2}}{{e}^{-3t}} & {} & {} \\\end{matrix}\]
Also, by (2) and (8) we have
$\begin{align} & v(0)=2V \\ & \frac{dv(0+)}{dt}=4{}^{V}/{}_{s} \\\end{align}$
Which may be used to obtain A1=5 and A2=-3, and thus
$\begin{matrix} v=5{{e}^{-t}}-3{{e}^{-3t}} & {} & {} \\\end{matrix}$
This overdamped case is easily sketched, as shown by the solid line of figure 2, by sketching the two components and adding them geographically.
Fig.2: Sketch of an Overdamped Response
The reason for the term overdamped may be seen from the absence of oscillations. The element values are such as to “damp out” any oscillatory tendencies. It is, of course, possible for the response to change signs once, depending on the initial conditions.
Underdamped Case
If the discriminant in (5) is negative, that is:
$\begin{matrix} L<4{{R}^{2}}C & \cdots & (9) \\\end{matrix}$
Then we have the underdamped case, where the natural frequencies are complex, and the response contains sine and cosine, which of course are oscillatory type functions. In this case, it is convenient to define a resonant frequency,
$\begin{matrix} {{\omega }_{o}}=\frac{1}{\sqrt{LC}} & \cdots & (10) \\\end{matrix}$
A damping coefficient,
$\begin{matrix} \alpha =\frac{1}{2RC} & \cdots & (11) \\\end{matrix}$
And a damped frequency,
$\begin{matrix} {{\omega }_{d}}=\sqrt{\omega _{o}^{2}-{{\alpha }^{2}}} & \cdots & (12) \\\end{matrix}$
Each of these is a dimensionless quantity “per second”. The resonant and damped frequencies are defined to be radians per second (rad/s) and the damping coefficient is nepers per second (Np/s).
Using these definitions, the natural frequencies, by (5), are
${{s}_{1,2}}=-\alpha \pm j{{\omega }_{d}}$
And therefore the response is
[stextbox id=”info” caption=”Under-damped Case”]$\begin{matrix} v={{e}^{-\alpha t}}({{A}_{1}}\cos {{\omega }_{d}}t+{{A}_{2}}\sin {{\omega }_{d}}t) & \cdots & (13) \\\end{matrix}$[/stextbox]
Which is oscillatory in nature, as expected.
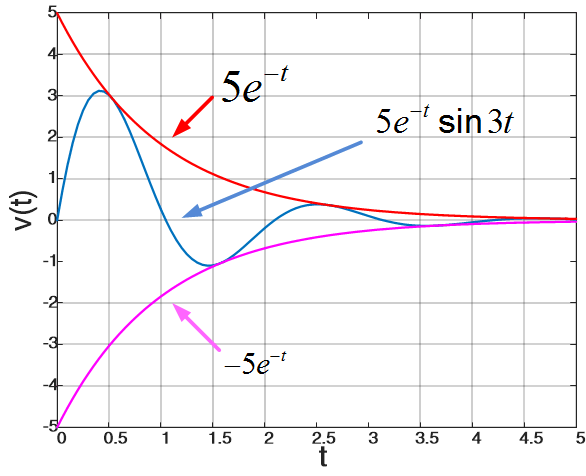
As an example, suppose R=5Ω, L=1H, C=1/10F, Vo=0, and Io=-3/2A. Then we have
$\begin{matrix} v={{e}^{-t}}({{A}_{1}}\cos 3t+{{A}_{2}}\sin 3t) & {} & {} \\\end{matrix}$
From the initial conditions we have
$\begin{align} & v(0)=0V \\ & \frac{dv(0+)}{dt}=15{}^{V}/{}_{s} \\\end{align}$
From which A1=0 and A2=5. Therefore the underdamped response is
$v=5{{e}^{-t}}\sin 3t$
The response is readily sketched if it is observed that since sin3t varies between +1 and -1, v must be a sinusoid that varies between 5e-t and -5e-t. The response is shown in figure 3, where it may be seen that is oscillatory in nature. The response goes through zero at the points where the sinusoid is zero, which is determined, in general, by the damped frequency ωd.
Fig.3: Sketch of an Underdamped Response
Critically damped case
When the discriminant in (5) is zero, we have the critically damped case, for which
$\begin{matrix} L=4{{R}^{2}}C & \cdots & (14) \\\end{matrix}$
In this case, the natural frequencies are real and equal, given by
$\begin{matrix} {{s}_{1,2}}=-\alpha ,-\alpha & \cdots & (15) \\\end{matrix}$
Where α is given by (11). The response is then
[stextbox id=”info” caption=”Critically-damped Case”]$\begin{matrix} v=({{A}_{1}}+{{A}_{2}}t){{e}^{-\alpha t}} & \cdots & (16) \\\end{matrix}$[/stextbox]
As an example, suppose R=1Ω, L=1H, C=1/4F, Vo=0, and Io=-1A. Then we have
\[\begin{matrix} v=({{A}_{1}}+{{A}_{2}}t){{e}^{-2t}} & {} & {} \\\end{matrix}\]
From the initial conditions we have
$\begin{align} & v(0)=0V \\ & \frac{dv(0+)}{dt}=4{}^{V}/{}_{s} \\\end{align}$
From which A1=0 and A2=4. Therefore the critically damped response is
$v=4t{{e}^{-2t}}$
This is easily sketched by plotting 4t and e-2t and multiplying the two together. The result is shown in figure 4.
Fig.4: Sketch of a critically damped Response
For every case in the parallel RLC circuit, the steady-state value of the natural response is zero, because each term in the response contains a factor of eat, where a<0.
- You May Also Read: Parallel RLC Circuit Problems with Solutions