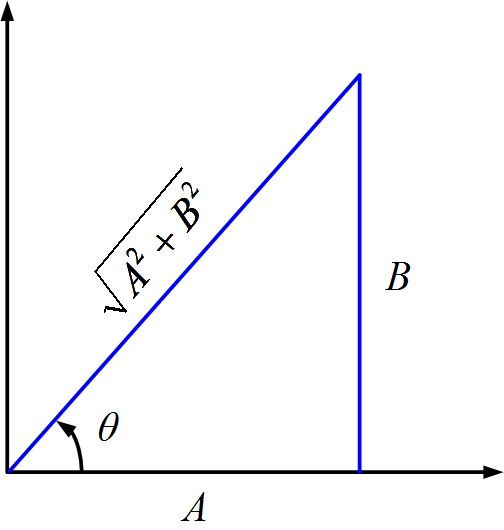Because of the importance of sinusoidal functions, I will devote this section to a review of some of their properties.
Let us being with the sine wave,
$\begin{matrix} v(t)={{V}_{m}}\sin (\omega t) & \cdots & (1) \\\end{matrix}$
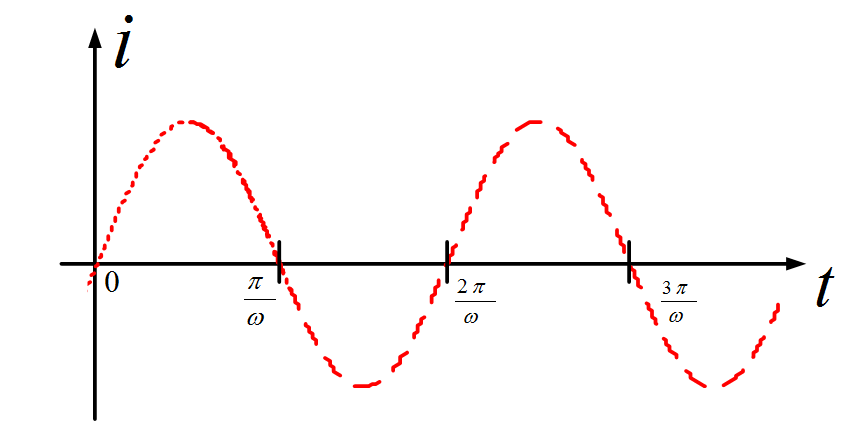
Which is sketched in figure (1). The amplitude of the sinusoid is Vm, which is the maximum value that the function attains. The radian frequency, or angular frequency, is ω, measured in radian per second (rad/s).
Fig.1: Sinusoidal Function
The sinusoid is a periodic function, defined generally by the property
$\begin{matrix} v(t+T)=v(t) & \cdots & (2) \\\end{matrix}$
Where T is the period. That is, the function goes through a complete cycle, or period, which is then repeated, every T seconds. In the case of the sinusoid, the period is
$\begin{matrix} T=\frac{2\pi }{\omega } & \cdots & (3) \\\end{matrix}$
As may be seen from (1) and (2). Thus in 1 second the function goes through 1/T cycles, or periods. Its frequency f is then
$\begin{matrix} f=\frac{1}{T}=\frac{\omega }{2\pi } & \cdots & (4) \\\end{matrix}$
Cycles per second, or hertz (abbreviated Hz). The relation between frequency and radian frequency is seen by (4) to be
$\begin{matrix} \omega =2\pi f & \cdots & (5) \\\end{matrix}$
A more general sinusoidal expression is given by
\[\begin{matrix} v(t)={{V}_{m}}\sin (\omega t+\phi ) & \cdots & (6) \\\end{matrix}\]
Where ϕ is the phase angle, or simply the phase. To be consistent, sinωt is in radians, ϕ should be expressed in radians. However, it is more convenient to specify ϕ in degrees. For example, we may write
$v(t)={{V}_{m}}\sin (2t+\frac{\pi }{4})$
Or
$v(t)={{V}_{m}}\sin (2t+{{45}^{o}})$
Interchangeably, even though the latter expression contains a mathematical inconsistencies.
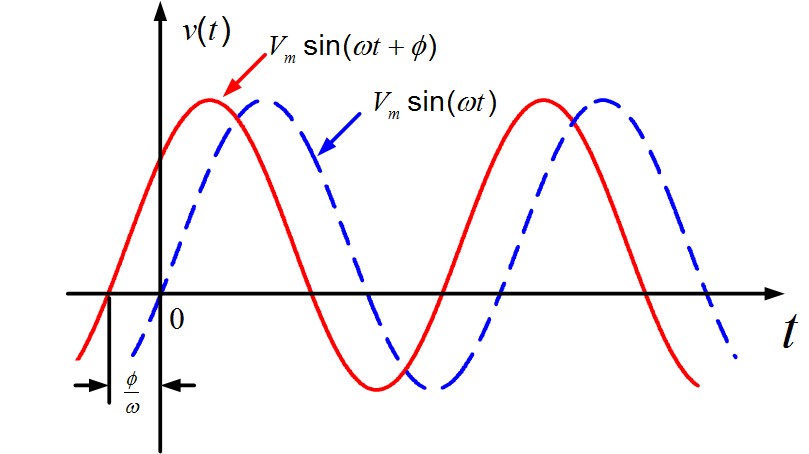
A sketch of (6) is shown in figure (2) by the solid line, along with a sketch of (1), shown dashed. The solid curve is simply the dashed curve displaced ϕ/ω seconds, or ϕ radians to the left. Therefore, points on the solid curve, such as its peaks, occur ϕ radians, or ϕ/ω seconds earlier than corresponding points on the dashed curve.
Fig.2: Two Sinusoids with different phases
Accordingly, we shall say that \[v(t)={{V}_{m}}\sin (\omega t+\phi )\] leads \[v(t)={{V}_{m}}\sin (\omega t)\] by ϕ radians (or degrees). In general, the sinusoid
\[{{v}_{1}}={{V}_{m1}}\sin (\omega t+\alpha )\]
Leads the sinusoid
\[{{v}_{2}}={{V}_{m2}}\sin (\omega t+\beta )\]
By α-β. An equivalent expression is that v2 lags v1 by α-β.
Example
As an example, consider
\[{{v}_{1}}=4\sin (2t+{{30}^{o}})\]
And
\[{{v}_{2}}=6\sin (2t-{{12}^{o}})\]
Then v1 leads v2 (or v2 lags v1) by 30-(-12) =42o.
Thus far we have considered sine functions rather than cosine functions in defining sinusoids. It does not matter which form we use since
$\begin{matrix} \cos (\omega t-\frac{\pi }{2})=\sin (\omega t) & \cdots & (7) \\\end{matrix}$
Or
$\begin{matrix} sin(\omega t+\frac{\pi }{2})=\cos (\omega t) & \cdots & (8) \\\end{matrix}$
The only difference between sines and cosines is thus the phase angles. For example, we may write (6) as
\[v(t)={{V}_{m}}cos(\omega t+\phi -\frac{\pi }{2})\]
To determine how much one sinusoid leads or lags another of the same frequency, we must first express both as since waves or cosine waves with positive amplitudes,
For example, let
\[{{v}_{1}}=4\cos (2t+{{30}^{o}})\]
And
\[{{v}_{2}}=-2\sin (2t+{{18}^{o}})\]
Then, since
\[-\sin (\omega t)=\sin (\omega t+{{180}^{o}})\]
We have
$\begin{align} & {{v}_{2}}=2\sin (2t+{{18}^{o}}+{{180}^{o}}) \\ & =2\cos (2t+{{18}^{o}}+{{180}^{o}}-{{90}^{o}}) \\ & =2\cos (2t+{{18}^{o}}+{{108}^{o}}) \\\end{align}$
Comparing this last expression with v1, we see that v1 leads v2 by 30o-180o=-78o, which is the same as saying v1 lags v2 by 78o.
The sum of a sine wave and a cosine wave of the same frequency is another sinusoid of that frequency. To show this, consider
$A\cos (\omega t)+B\sin (\omega t)=\sqrt{{{A}^{2}}+{{B}^{2}}}\left[ \frac{A}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\cos (\omega t)+\frac{B}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\sin (\omega t) \right]$
Which by figure (3), may be written as
$A\cos (\omega t)+B\sin (\omega t)=\sqrt{{{A}^{2}}+{{B}^{2}}}\left[ \cos (\omega t)\cos (\theta )+\sin (\omega t)sin(\theta ) \right]$
By a formula from trigonometry, this is
$\begin{matrix} A\cos (\omega t)+B\sin (\omega t)=\sqrt{{{A}^{2}}+{{B}^{2}}}\cos (\omega t-\theta ) & \cdots & (9) \\\end{matrix}$
Where, by figure (3),
$\begin{matrix} \theta ={{\tan }^{-1}}\frac{B}{A} & \cdots & (10) \\\end{matrix}$
Fig.3: Triangle useful in adding two sinusoids
A similar result may be established if the sine and cosine terms have phase angles other than zero, indicating that, in general, the sum of two sinusoids of a given frequency is another sinusoid of the same frequency.
https://www.youtube.com/watch?v=OGI-065RhFo
- You May Also Read: Phasors in Electric Circuits