Source transformation is a circuit analysis technique in which we transform voltage source in series with resistor into a current source in parallel with the resistor and vice versa.
A highly valuable byproduct of Thevenin’s and Norton’s theorem is the technique of source transformation. Source transformation is based on the observation that if a Thevenin’s network and Norton’s network are both equivalent to a particular source network, then they must also equivalent to each other. This observation allows you to simply an analysis by converting a voltage source with series resistance to an equivalent current source with parallel resistance, or vice versa.
- You May Also Read: Thevenin’s Theorem with Solved Examples
Source conversion may be applied to portions of a circuit to simplify intermediate calculations. Going even further, repeated source conversions may reduce a circuit to all-series or all-parallel form. Conversions may also be applied to controlled sources as well as to independent sources.
- You May Also Read: Norton’s Theorem with Solved Examples
In the development of practical voltage sources and current sources, many similarities should have been noticed -such as internal resistance, voltage, and current characteristics. These similarities lead one to ask if it is possible to interchange one practical source for the other and retain the same results at the load. This forms the basis of source transformation.
If the same value of load resistance RL is connected to the circuits of the following figure, the load current flowing in circuit (a) is;
${{I}_{L}}=\frac{{{E}_{s}}}{{{R}_{s}}+{{R}_{L}}}~~~~\text{ }\cdots \text{ }~~~~~~~\left( 1 \right)$
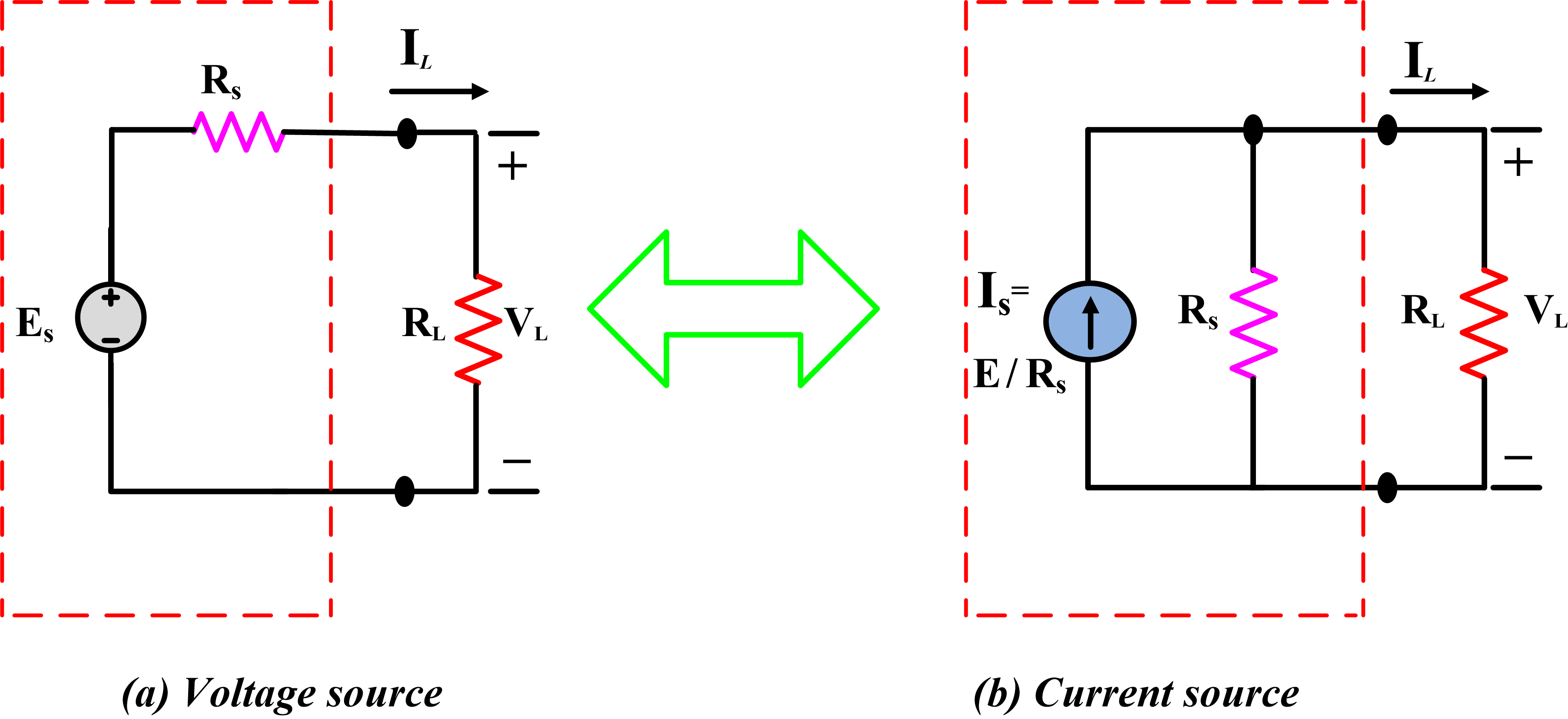
Figure 1. Source Transformation
And the load current flowing in circuit (b) is
${{I}_{L}}=\frac{{{R}_{s}}}{{{R}_{s}}+{{R}_{L}}}*{{I}_{s}}~~~~\text{ }\cdots \text{ }~~~~~\left( 2 \right)$
To produce the same effect at the load, equations (1) and (2) must be equal.
$\frac{{{E}_{s}}}{{{R}_{s}}+{{R}_{L}}}=\frac{{{R}_{s}}}{{{R}_{s}}+{{R}_{L}}}*{{I}_{s}}$
Thus establishing the result that
${{E}_{s}}={{I}_{s}}{{R}_{s}}$
Or
${{I}_{s}}=\frac{{{E}_{s}}}{{{R}_{s}}}$
The value of internal resistance for practical voltage and the current source does not change. Although these equations have been derived for AC conditions. They are also equally applicable to DC circuits. Note that the same values of voltage, current and power may be obtained at the output terminals by either a practical voltage or a practical current source.
Impossible Source Transformation
These are two certain situations when we cannot do source transformation.
1.When voltage source has zero resistance in this case,
${{I}_{s}}=\frac{{{E}_{s}}}{R}$
$R=0$
So;
${{I}_{s}}=\infty $
2.When current source has infinite resistance, in this case
${{V}_{s}}={{I}_{s}}R$
$R=\infty $
So,
${{V}_{s}}=\infty $
Source Transformation Example
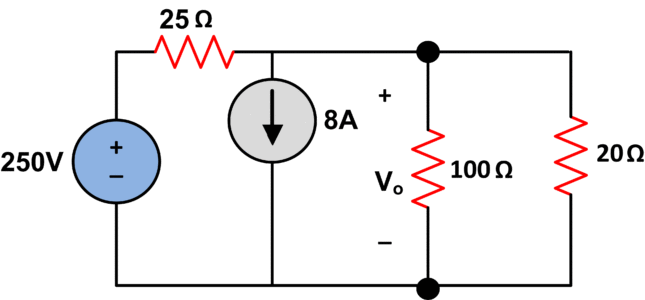
Find Vo using source Transformation
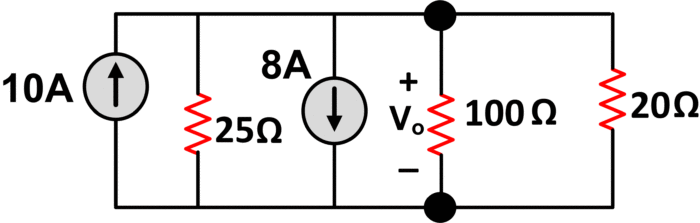
We convert 250V voltage source into 10A current source.
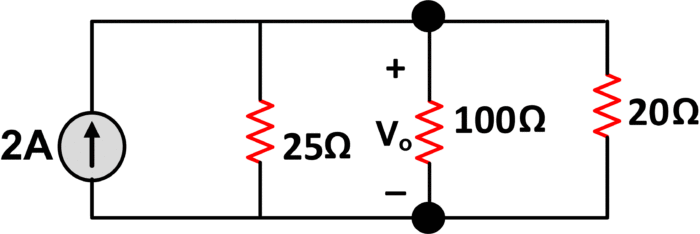
Combining both current sources, we obtain
Adding resistance in a parallel manner will give us the following circuit
Finally,
${{V}_{0}}=20V~$
Source Transformation Example with Dependent Source
Let’s find v2 in the following circuit using source transformation.
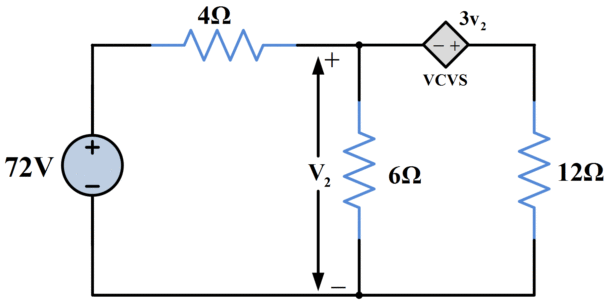
Figure.2: Source Transformation Example with Dependent Source
Solution
The 72-V source and the 4Ω series resistance convert to a parallel structure with source current of
\[~72V/4\Omega =18A\]
The VCVS and the 12 Ω series resistance likewise convert to a parallel structure with source current of
\[~3{{v}_{2}}/12\text{ }\Omega =0.25S*{{v}_{2}}\]
So, the VCVS becomes a VCCS whose transconductance is 0.25S. The resulting diagram in figure 3 still has the control voltage v2 in place, as required.
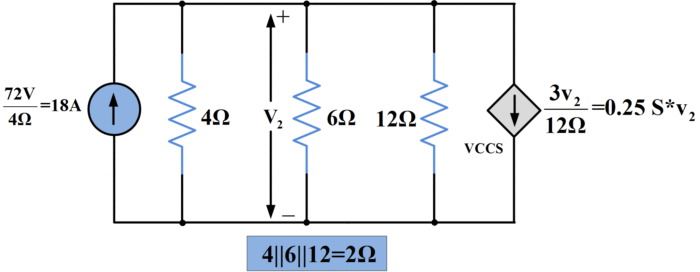
Figure.3
But now all three resistances can be combined as 4||6||12=2 Ω. This parallel equivalent resistance carries the net current from the sources, and so
\[{{V}_{2}}=2\left( 18-0.25{{v}_{2}} \right)\]
Solving for V2 yields
\[{{V}_{2}}=36/1.5=24V\]
Source Transformation Key Takeaways
– Source transformation is a technique used in circuit analysis to simplify complex circuits by converting voltage sources into current sources, and vice versa.
– The technique allows for the combination of series and parallel resistances, resulting in simpler circuit configurations.
– Source transformation is based on the principle of equivalence, where the transformed circuit maintains the same voltage-current relationships as the original circuit.
– The transformation involves replacing a voltage source with an equivalent current source, or replacing a current source with an equivalent voltage source, while keeping the other elements of the circuit unchanged.
– The transformed circuit can be easier to analyze using methods such as Ohm’s law, Kirchhoff’s laws, and other circuit analysis techniques.
– Source transformation is particularly useful in solving circuits with multiple sources and resistances, as it simplifies the circuit structure and reduces complexity.
– The technique can help in determining current and voltage values, power dissipation, and overall circuit behavior.
– It is important to exercise caution when applying source transformation, ensuring that the transformation maintains the same voltage-current relationships and that the circuit laws and principles are properly applied during analysis.
Source Transformation FAQs
What is source transformation in circuit analysis?
Source transformation is a technique used in circuit analysis to simplify complex circuits by converting voltage sources into current sources, or vice versa.
Why is source transformation used?
Source transformation is used to simplify circuit configurations, making them easier to analyze and solve. It allows for combining series and parallel resistances and helps in applying various circuit analysis techniques.
How does source transformation work?
Source transformation works by replacing a voltage source with an equivalent current source, or replacing a current source with an equivalent voltage source, while keeping the other elements of the circuit unchanged.
What are the benefits of source transformation?
Source transformation simplifies circuit structures, reduces complexity, and enables the use of circuit analysis methods such as Ohm’s law, Kirchhoff’s laws, and other techniques. It can make it easier to determine current and voltage values and understand overall circuit behavior.
When should source transformation be applied?
Source transformation is particularly useful when dealing with circuits that have multiple sources and resistances. It is applied to simplify the circuit and facilitate analysis.
Are there any limitations or considerations when using source transformation?
It is important to ensure that the transformed circuit maintains the same voltage-current relationships as the original circuit. Proper application of circuit laws and principles is crucial during analysis. Care must be taken to accurately apply the technique and consider any specific limitations or restrictions of the circuit components involved.
Can source transformation be used in all circuits?
Source transformation can be applied to most circuits with resistive components, as long as the voltage-current relationships are maintained. However, there may be specific cases or circuit configurations where source transformation is not applicable or yields inaccurate results.
Are there alternative techniques to source transformation?
While source transformation is a widely used technique, there may be alternative approaches to simplify and analyze circuits, depending on the specific circuit characteristics and analysis objectives. Other methods such as network theorems, superposition, and nodal/mesh analysis can also be employed.