Thevenin’s Theorem Tutorial | Thevenin's Equivalent Circuit

What is the Thevenin’s Theorem?

Thevenin’s Theorem states that any two-terminal linear network containing resistances and voltage sources and/or current sources may be replaced by single voltage source in series with a single resistance. The emf of the voltage source is the open circuit emf at the network terminals, and the series resistance is the thevenin’s equivalent resistance between the network terminals when sources are set to zero.

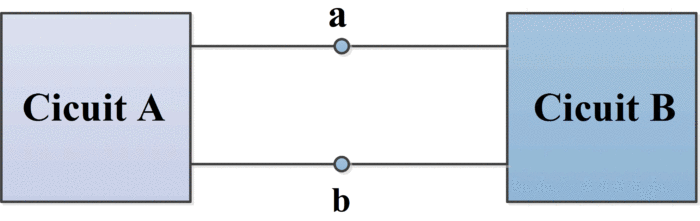
Suppose we are given an arbitrary circuit containing any or all of the following elements: resistors, voltage sources, current sources (the source can be dependent as well as independent). Let us identify a pair of nodes, say node a and b, such that the circuit can be partitioned into two parts as shown in figure 1.

Figure.1: Circuit partitioned into two parts

Furthermore, suppose that circuit A contains no dependent source that is dependent on a variable in circuit B and vice versa. Then, we can model circuit A by an appropriate independent voltage source, call it V_oc that is connected in series with an appropriate resistance, call it R_TH. This series combination of a voltage source and a resistance is called the Thevenin’s equivalent of circuit A. in other words, circuit A in figure 1 and the circuit in the shaded box in figure 2 have the same effect on circuit B. This result is known as Thevenin’s theorem and is one of the most useful and significant concepts in circuit theory.

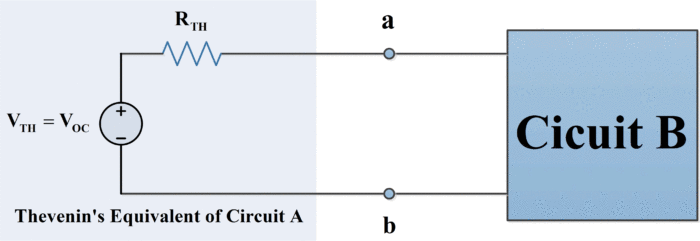
Figure.2: Thevenin’s Equivalent Circuit

Circuit B (which is often called a load) may consist of many circuit elements, a single element (a load resistor), or no element.

You May Also Read: Norton’s Theorem with Solved Examples

How to Find the Equivalent Voltage of a Thevenin Circuit?

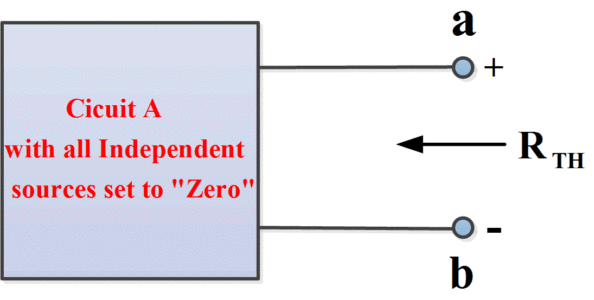
To obtain the voltage V_oc– called the open circuit voltage- remove circuit B from circuit A, and determine the voltage between node a and b ( where the + is at node a). This voltage, as shown in figure 3(a), is V_oc.

Figure.3 (a): How to Find the Equivalent Voltage of a Thevenin Circuit

How to Find the Equivalent Resistance in Thevenin’s Theorem?

There are several ways to find the Thevenin’s equivalent resistance, which are given below:
1. To obtain the resistance R_TH– called the Thevenin’s equivalent resistance of circuit A:
i) Remove circuit B from circuit A.
ii) Set all independent sources in circuit A to zero. (A zero voltage source is equivalent to a short circuit, and zero current source is equivalent to an open circuit).
iii) Determine the resistance between nodes a and b- this is R_TH– as shown in figure 3(b).

Figure.3 (b): Determination of Thevenin’s Equivalent Resistance R_TH

2. Short-circuit the terminals a and b then find the short-circuit current I_sc. The Thevenin equivalent resistance is given by

\[{{\text{R}}_{\text{th}}}\text{= }{{\text{V}}_{\text{oc}}}\text{/}{{\text{I}}_{\text{sc}}}\text{= }{{\text{V}}_{\text{th}}}\text{/}{{\text{I}}_{\text{sc}}}\]

3. When the source network has a ladder structure and contains no controlled (dependent) sources, R_TH is easily found by series-parallel reduction of the dead network.

When the source network contains controlled sources, the Thevenin’s resistance can be found using the method represented by figure 4.

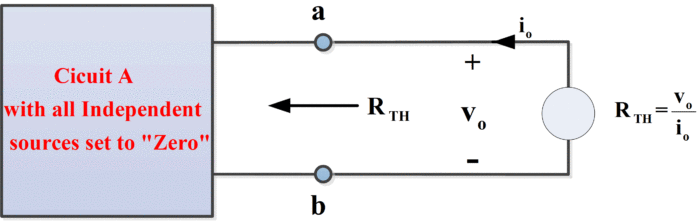
Figure.4: How to Find the Thevenin’s Equivalent Resistance

Here, the dead source network has been connected to an external test source. This test source may be any independent voltage or current source that establishes v_o at the terminals. Since the dead network contains only resistors and controlled sources, and since R_TH equals the equivalent resistance of the dead network, the equivalent resistance theorem tells us that

\[{{R}_{TH}}={{v}_{o}}/{{i}_{o}}\]

Thevenin’s Theorem Solved Example with Voltage Source

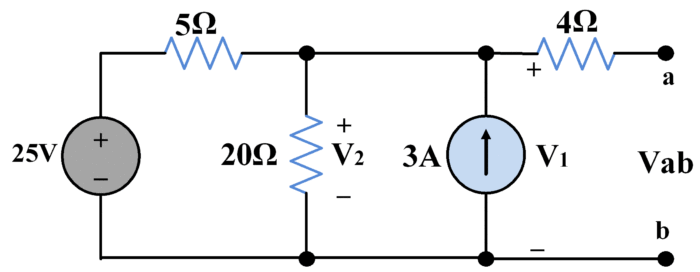
Find Thevenin equivalent circuit of the following network.

By applying nodal voltage method,

$\frac{{{V}_{1}}-25}{5}+\frac{{{V}_{1}}}{20}-3=0$

${{V}_{1}}=32~V$

${{V}_{th}}=32V$

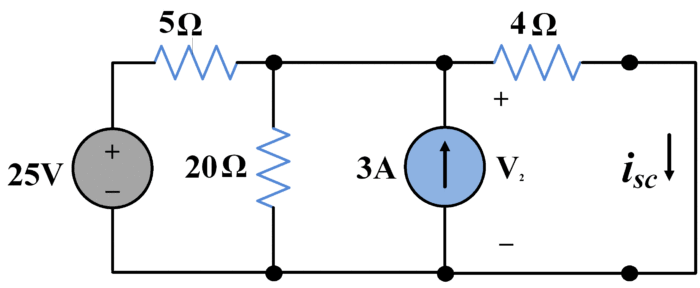
To find short circuit current, we short-circuited terminals a and b as shown in the following figure:

Again using nodal voltage method,

$\frac{{{V}_{2}}-25}{5}+\frac{{{V}_{2}}}{20}-3+\frac{{{V}_{2}}}{4}=0$

${{V}_{2}}=16~V$

${{I}_{sc}}=\frac{{{V}_{2}}}{4}=\frac{16}{4}=4A$

So,

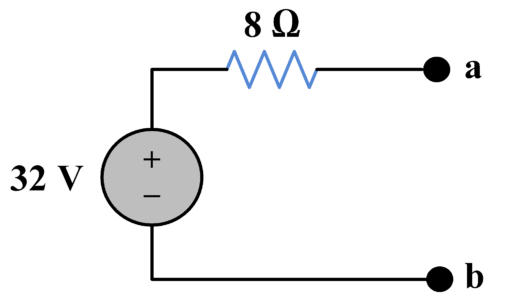
${{R}_{th}}=\frac{{{V}_{th}}}{{{I}_{sc}}}=\frac{32}{4}$

${{R}_{th}}=8~\Omega $

Now, we have following equivalent circuit:

Thevenin’s Theorem Solved Problem with Dependent Sources

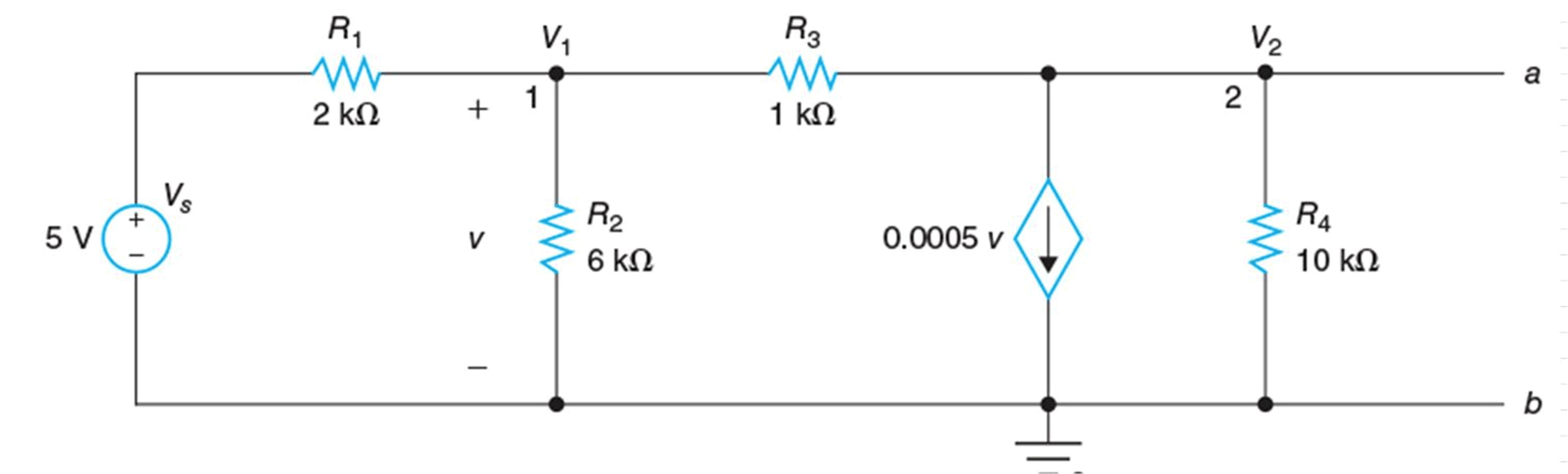
Consider a circuit shown in the following figure. We will determine V_thand R_th across terminals a and b of the circuit.

Applying KCL at node 1:

\[\begin{matrix} \frac{{{V}_{1}}-5}{2000}+\frac{{{V}_{1}}}{6000}+\frac{{{V}_{1}}-{{V}_{2}}}{1000}=0 & \cdots & (1) \\\end{matrix}\]

Multiply (1) by 6000 yields

\[3{{V}_{1}}\text{- }15\text{ }+\text{ }{{V}_{1}}+\text{ }6{{V}_{1}}\text{ -}6{{V}_{2}}=\text{ }0\]

\[10{{V}_{1}}=\text{ }6{{V}_{2}}+\text{ }15\]

\[{{V}_{1}}=\text{ }0.6{{V}_{2}}+\text{ }1.5\]

Applying KCL at node 2:

\[\begin{matrix} \frac{{{V}_{2}}-{{V}_{1}}}{1000}+0.0005{{V}_{1}}+\frac{{{V}_{2}}}{10000}=0 & \cdots & (2) \\\end{matrix}\]

Multiply (2) by 10000 yields

\[10{{V}_{2}}\text{ -}10{{V}_{1}}+\text{ }5{{V}_{1}}+\text{ }{{V}_{2}}=\text{ }0\]

\[11{{V}_{2}}\text{ -}5{{V}_{1}}=\text{ }0\]

\[11{{V}_{2}}\text{- }5(0.6{{V}_{2}}+\text{ }1.5)\text{ }=\text{ }0\]

\[8{{V}_{2}}=\text{ }7.5\]

Finally we have

\[{{V}_{th}}=\text{ }{{V}_{oc}}=\text{ }{{V}_{2}}=\text{ }7.5/8\text{ }=\text{ }0.9375\text{ }V\]

Now, we have dependent source, so method 1 cannot be used for finding Thevenin’s Equivalent resistance Rth. Either Method 2 or Method 3 can be utilized here. We will prefer to employ second method. Terminals a and b are to be shorted as shown in the following figure and V₂ = 0.

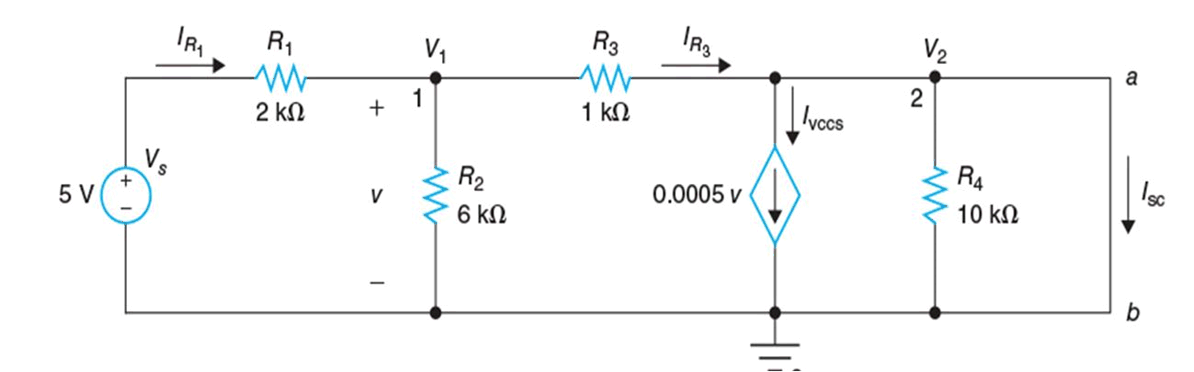
Applying KCL at node 1:

\[\begin{matrix} \frac{{{V}_{1}}-5}{2000}+\frac{{{V}_{1}}}{6000}+\frac{{{V}_{1}}}{1000}=0 & \cdots & (3) \\\end{matrix}\]

Multiplying (3) by 6000 yields:

\[3{{V}_{1}}\text{- }15\text{ }+\text{ }{{V}_{1}}+\text{ }6{{V}_{1}}=\text{ }0\]

\[10{{V}_{1}}=\text{ }15\]

\[{{V}_{1}}=\text{ }1.5\text{ }V\to \text{ }v\text{ }=\text{ }{{V}_{1}}=\text{ }1.5\text{ }V\]

The current through R₃ (⟶) is given by

\[{{I}_{{{R}_{3}}}}=\text{ }{{V}_{1}}/{{R}_{3}}=~1.5\text{ }V/1k\Omega =\text{ }1.5mA\]

The current through VCCS (↓) is given by

\[{{I}_{VCCS}}=\text{ }0.0005{{V}_{1}}=~0.0005*1.5\text{ }A\text{ }=\text{ }0.75mA\]

Now, short-circuit current would be

\[{{I}_{sc}}=\text{ }{{I}_{{{R}_{3}}}}\text{ -}{{I}_{VCCS}}=\text{ }1.5mA\text{ -}0.75mA=\text{ }0.75mA\]

And Thevenin’s equivalent resistance is

\[{{R}_{th}}={{V}_{th}}/{{I}_{sc}}=\text{ }0.9675\text{ }V/0.75mA=\text{ }1.25\text{ }k\Omega \]

Thevenin’s Theorem Steps

Following steps are being used to determine Thevenin’s equivalent circuit.

The portion of circuit considered as load is removed
The open circuit voltage V_oc is calculated at terminals.
To calculate R_th

Short circuit all independent voltage sources.
Open circuit all independent current sources.

Draw equivalent circuit, connect the load and determine load current.

Thevenin’s Theorem | Thevenin’s Equivalent Circuit