Transfer Functions Representation
Consider a fixed single-input/single-output linear system with input u(t) and output y(t) given by the differential equation
$\begin{matrix} \overset{..}{\mathop{y}}\,+6\overset{.}{\mathop{y}}\,+5y=4\overset{.}{\mathop{u}}\,+3u & \cdots & (1) \\\end{matrix}$
Applying the Laplace transform to both sides of (1) with zero initial conditions, we obtain the transfer function of the system from the input U (s) to the output Y(s) in TF form as the ratio of polynomials:
$\begin{matrix} G(s)=\frac{4s+3}{{{s}^{2}}+6s+5} & \cdots & (2) \\\end{matrix}$
Alternatively, this transfer function can be expressed in terms of its zeros zi, poles pj, and gain K in the factored, or Zero-Pole (ZP) form, as
$\begin{matrix} G(s)=\frac{4(s+0.75)}{(s+1)(s+5)} & \cdots & (3) \\\end{matrix}$
Which shows that G(s) has a single zero at s = -0.75, two poles at s = -1 and -5, and a gain of 4.
Transfer Function Using Numerator and Denominator Coefficients
If we know the numerator and denominator polynomials of G(s), we can represent the model in MATLAB by creating a pair of row vectors containing the coefficients of the powers of s, in descending order, of the numerator and denominator polynomials. For the transfer function in (2), we would enter numG = [4 3] and denG = [1 6 5].
If the transfer function is known in terms of its zeros, poles, and gain, we can create the model by entering column vectors for the zeros and poles, and enter the gain as a scalar. Then the model is represented by these three quantities, which can be used as arguments in commands for performing calculations. To create the system described in (3), we would enter the commands zG = -0.75, pG = [-1; -5],and kG = 4.
When a model has been described in MATLAB in either one of these forms, the Control System Toolbox provides several functions to obtain the description in the other form.
Commands to Create Transfer Functions
For example, if the numerator and denominator polynomials are known as the vectors numG and denG, we merely enter the MATLAB command [zz, pp, kk] = tf2zp (numG, denG). The result will be the three-tuple [zz, pp, kk] , which consists of the values of the zeros, poles, and gain of G(s), respectively. Alternatively, if the zeros, poles, and gain are known as the column vectors zG and pG and the scalar kG, we would enter the command [num, den] = zp2tf (zG, pG, kG) .
Transfer Function Graphical Representation
Once we have the system model in either the TF or the ZP form, we can obtain a graphical representation of the transfer functions poles and zeros by using the pzmap command from the Control System Toolbox. The two forms of the command that are applicable to transfer-function models are pzmap(numG,denG) and pzmap(pG, zG), where in the first case the arguments are row vectors and in the latter case, the arguments are column vectors. In either case, a region of the s-plane is shown with the zeros indicated by “O” and the poles by “X”.
Transfer Function Matlab Example
Convert G(s) to Factored Form
Find the transfer function in both the polynomial (TF) and factored (ZP) forms for the fourth-order system whose differential equation is
\[\overset{….}{\mathop{y}}\,+3\overset{…}{\mathop{y}}\,+4\overset{..}{\mathop{y}}\,+2.5\overset{.}{\mathop{y}}\,+0.8y=3\overset{..}{\mathop{u}}\,+5\overset{.}{\mathop{u}}\,+7u\]
Solution
Taking the Laplace transform of the differential equation with zero initial conditions, we obtain the polynomial form of the transfer function as
\[G(s)=\frac{3{{s}^{2}}+5s+3}{{{s}^{4}}+3{{s}^{3}}+4{{s}^{2}}+2.5s+0.8}\]
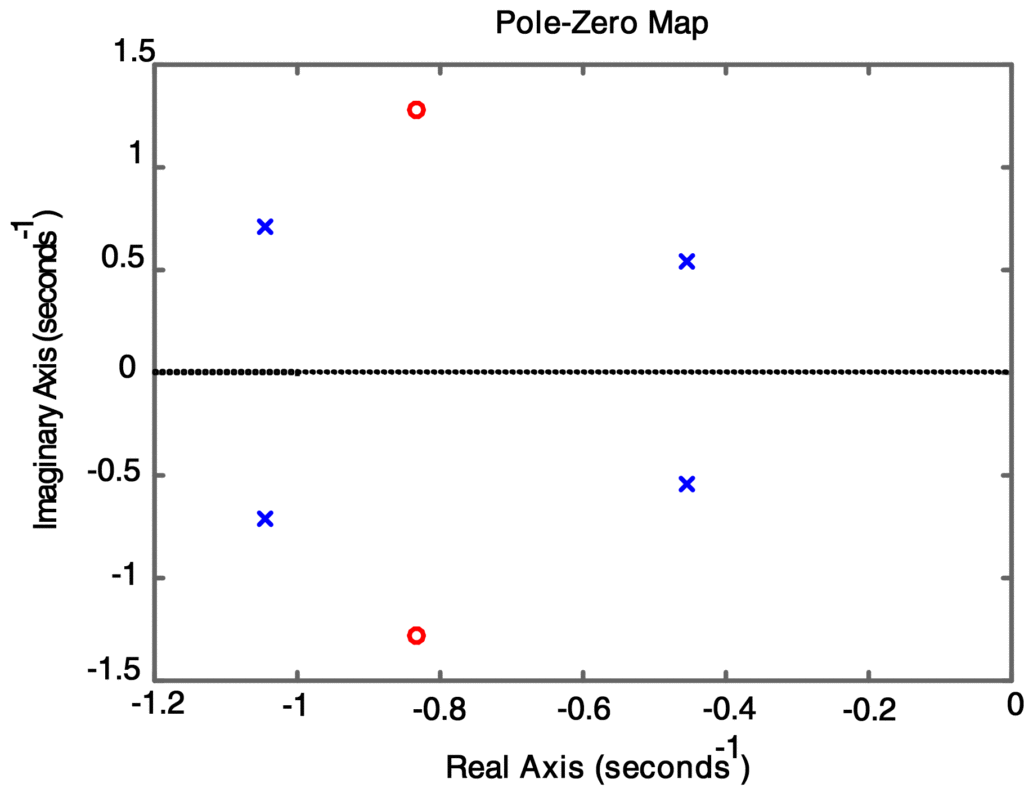
The MATLAB commands in Script 1 will create the polynomial form of G(s) and then use it to determine the factored form. From the numerical output we find that G(s) has zeros at s = -0.8333± j1.2802, poles at s == -0.4548±j0.5420 and s = -1.0452±j0.7110, and a gain of 3.
Matlab Code to Find the Transfer Function
% Script 1: Matlab Code to Find the transfer function %in both the polynomial (Transfer-Function) and factored (Zero-Pole) forms numG = [3 5 7] % enter transfer function numerator denG = [1 3 4 2.5 0.8] % ...and denominator polynomials % convert to factored (ZP) form [zz,pp,kk] = tf2zp(numG,denG) pzmap(numG,denG) % pzmap from TF form pzmap(pp,zz) % pzmap from ZP form