The goal of this module is to provide learners with tools for reducing Boolean algebra expressions to their simplest form.
Objectives
The learner will be able to:
- Reduce Boolean expressions using the 14 Boolean rules.
- Simplify complex Boolean algebra expressions using the 14 Boolean rules and apply DeMorgan’s Theorem.
- Carry out logic simplification using a 3-variable Karnaugh map.
- Simplify Boolean algebraic expressions using a 4-variable Karnaugh map.
Orienting Questions
- How do you reduce Boolean expressions using the basic Boolean identities?
- How do you simplify complex Boolean expressions?
- What are Karnaugh maps?
- How do you simplify and solve a Boolean expression having three variables using a Karnaugh map?
- How do you simplify and solve a Boolean expression having four variables using a Karnaugh map?
Introduction
Any Boolean expression can be reduced to its simplest form from more complex expressions. The purpose of this module is to apply Boolean rules and laws with the addition of DeMorgan’s theorem to simplify these complex Boolean expressions. We will also address an alternate method of logic simplification known as Karnaugh mapping. This method utilizes a mapping technique to represent all of the terms in the complex Boolean expression. All the similar terms in the mapped expression are canceled out leaving the reduced Boolean expression.
Boolean rules
Before we begin our examples to understand logic simplification, we should show all of the Boolean laws we will use to reduce our logic functions. We will address each one of these by numbers as we progress through our examples so we can see how each is applied.
Some basic Boolean Rules:
- AB = BA Commutative Law for multiplication
- A + B = B + A Commutative Law for addition
- A ∙ 0 = 0
- A ∙ 1 = A
- A ∙ A = A
- A + 0 = A
- A + 1 = 1
- A + A = A
- A.$\overline{A}$=0
- A + $\overline{A}$ = 1
- $\overline{\overline{A}}$ = A
- A + AB = A
- A + $\overline{A}$ B = A + B
- (A+B)(A+C) = A + BC
DeMorgan’s Theorem
- \[\overline{A\bullet B}=\overline{A}+\overline{B}\]
- \[\overline{A+B}=\overline{A}\bullet \overline{B}\]
Logic Simplification Examples
Let’s do some examples now. Make sure when you work these problems, that you work down the page showing all work and noting which rule number is applied.
Logic simplification using Demorgan’s Theorem
As in the previous section, we will address the more complicated logic simplification using DeMorgan’s theorem through examples. The illustration of these problems through examples is the best way to understand the power of the Theorems applied and creating a simple logic expression from a more complex creation of logic.
Let’s do some examples now, make sure when you work these problems, that you work down the page showing all work and noting which rule number is applied as shown below.
Karnaugh Mapping
Another alternative method used for simplifying Boolean logic expressions is Karnaugh mapping. There are several ways to represent Karnaugh maps to solve logic expressions. The representation that we will use will be the letter designation for each cell in a Karnaugh map. The possible logic states could also be represented in each cell, however, we will address those possibilities in the supplement video supplied at the end of this module. We will address a 3-variable Karnaugh map and a 4-variable Karnaugh map. We will then show how to tackle these problems through a few examples.
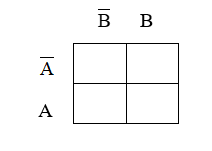
Mapping 2 binary variables
In order to understand Karnaugh mapping, we must address the simplest example of mapping a basic 2 binary variable truth table to a map. Figure 1 shows a two variable binary truth table.
| A | B | X |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Fig. 1 Two variable binary truth table
We can map this truth table on a map. See figure 2 for an example.
Fig. 2 Two variable binary truth table on a map
In the example provided in figure 3, note the location of each entry on the truth table to that on the map.
Fig. 3 Truth Table
Whether or not each entry in the map is a 1 or 0 is determined by the output column X in the truth table.
Before we can map Boolean expressions, we must outline some rules (note: these rules will be clearer as we do a few examples)
- Fill in the map with 1’s or 0’s on the map based on truth table or terms in Boolean expression given
- Group the 1’s (not 0’s) on the map subject to
- Group the 1’s in rectangles or squares on the map
- Groups sizes are 1’s grouped in 1, 2’s, 4 ’s, 8’s, 16’s….etc.
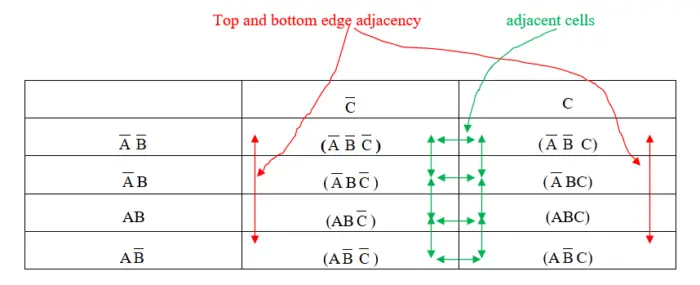
- Groups of 1’s are determined by their adjacency. Adjacent cells are defined as those ones next to each other (above and below, and left-right edges) on any of its four sides. Cells that are diagonal to each other are not adjacent to each other, therefore, are not grouped. The top and bottom edges of the map entries are also considered adjacent.
- Finally, we will list the individual groups mapped top over bottom. A’s,B’s,C’s for each group in their own column. If there is no change in the letter, it drops down, if a letter and its complement is in the same column, they cancel and do not appear in the final expression.
- The remaining terms in each group are OR’ed together to yield the final expression.
3-Variable Karnaugh map
A 3-variable Karnaugh map consists of logic expressions whose terms contain only A, B and C. They could contain terms like x, y, and z, but the designation of terms does not matter because the setup is the same. The setup for the map is an array constructed such that all possibilities are represented on the map.
Fig. 4: 3-variable Karnaugh Map
Notice the new form of the array as opposed to the 2-variable array addressed before. Once the array is populated with all the possible entries, we can then simplify the expressions following the guidelines outlined earlier. The best way to understand Karnaugh mapping, like logic simplification using Boolean rules before, is through examples. Let’s do a few.
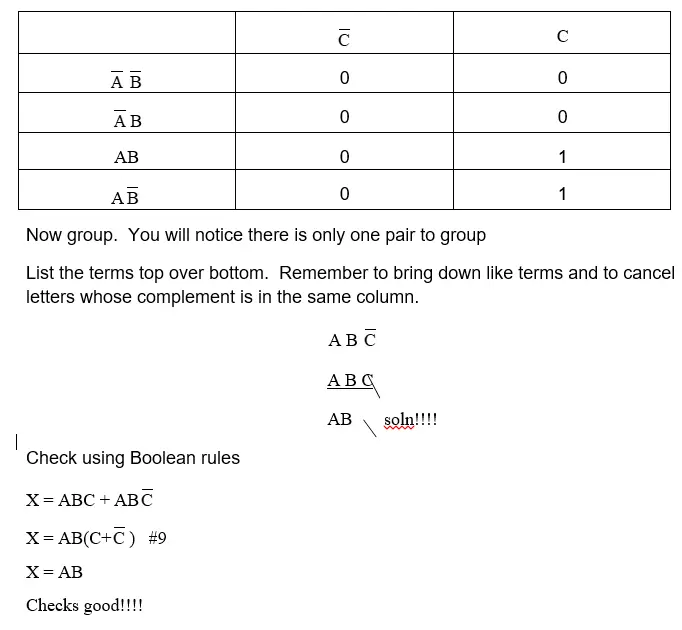
3-variable Karnaugh Map Example
X = ABC + AB$\overline{C}$
Create the 3-variable map
Place 1’s everywhere each term is represented. Place 0’s in all other non-relevant positions
Example #2 Following the same procedure as before
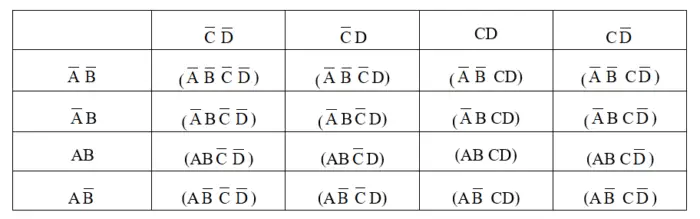
4-Variable Karnaugh Map
A 4-variable Karnaugh map consists of logic expressions whose terms contain only A, B, C, and D. They could contain terms like w, x, y, and z, but just like before, the designation of terms does not matter because the setup is the same. The setup for the map is an array constructed such that all possibilities are represented on the map. The 4-variable Karnaugh map will, of course, have more logic possibilities, thus a larger array to represent those possibilities.
The rules that are used for the 3-variable map is the same as the 4-variable map. The 4-variable map takes the following form.
4-variable Karnaugh Map of Example
Let’s look at an example of a 4-variable Karnaugh Map