The article introduces the working principle of a potentiometer, explaining how it measures and compares potential differences without drawing current. It outlines its construction, operational theory, and typical applications such as measuring emf and serving as a potential divider.
Potentiometer Principle
The potential difference across any length of wire of uniform cross-section area is directly proportional to its length where a constant current flows through it.
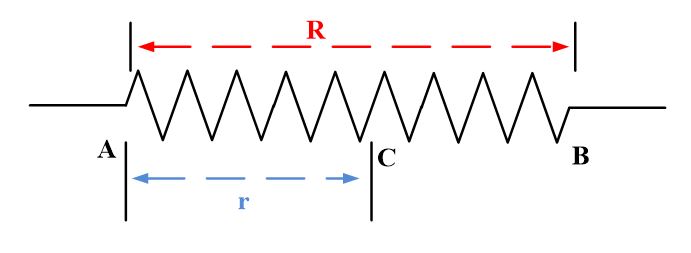
A potentiometer consists of a resistance R in the form of a wire on which a terminal C can slide as shown in Fig.
The resistance between A and C can be varied from 0 to R as the sliding contact is moved from A to B. Let a battery of emf E be connected across R as shown in Fig.
The current flowing through it is given by
$I=\frac{E}{R}~~~~~\cdots \text{ }~~~~\left( 1 \right)$
If we represent the resistance between A and C by r, then the potential drop between these points will be,
$V=Ir~~~~\text{ }\cdots \text{ }~~~~\left( 2 \right)$
Putting the value of I from eq (1) into (2) we obtain,
$V=\frac{E}{R}*r$
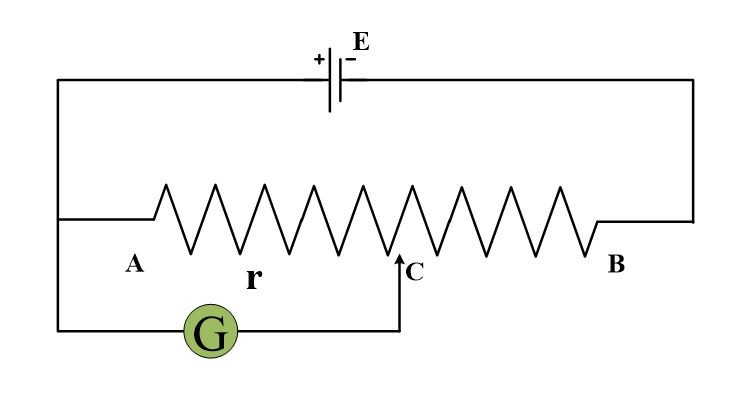
Where C is moved from A to B, r varies from 0 to R and potential drop between A and C changes from 0 to E. Such an arrangement is known as a potential divider. A potential divider can be used to determine the unknown emf of a source by using the circuit given below.
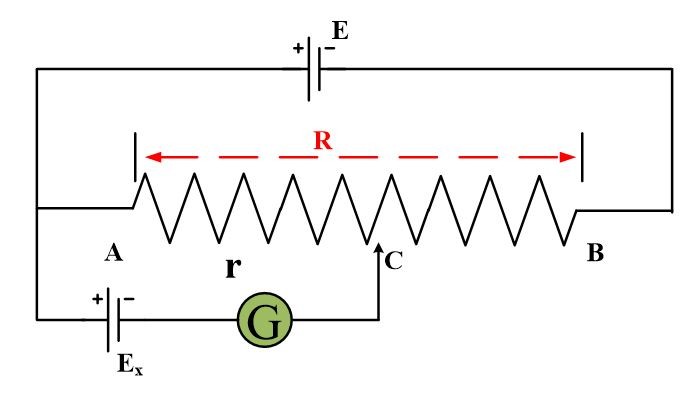
The figure shows that R is in the form of a straight wire of uniform area of cross-section. A source of potential, whose Ex emf is to be measured is connected between A and sliding contact C through a galvanometer G. The positive terminal of Ex and that of the potential divider are connected to the same point A.
“If the point C and negative terminal of Ex are at the same potential then the two terminals of galvanometer will be at the same potential and no current will flow through the galvanometer.”
Therefore, in order to measure the potential Ex, the position of C is so adjusted that the galvanometer shows no deflection. Under this condition, the emf Ex is equal to the potential difference between A and C whose value ($\frac{E}{R}*r$) is known.
In the case of wire of uniform area of cross-section, the resistance is proportional to the length of a wire. Therefore unknown is given by;
${{E}_{x}}=\frac{r}{R}*E$
Or
${{E}_{x}}=\frac{l}{L}*E$
Where L is the length of wire AB and l is a length of wire from A to C. The unknown emf Ex should not exceed E-value, otherwise, the null condition will not be obtained.
Uses of Potentiometer
- It can be used to determine the emf of a cell.
- It can be used to compare the emf of two cells.
- It can be used as a continuously potential divider.
- You May Also Read: Impedance Measurement Theory
Potentiometer Variable Resistor Key Takeaways
The potentiometer is a crucial instrument in electrical measurements due to its ability to provide accurate and reliable results without drawing current from the circuit. Its applications—such as measuring the emf of a cell, comparing emfs, and functioning as a continuous potential divider—make it indispensable in both laboratory experiments and practical electrical engineering tasks where precision and sensitivity are essential.