The area within the hysteresis loop is a product of B and H and this area represents the energy per unit volume that must be used per magnetization cycle to move the domains.
Hysteresis Loss
With appropriate constants, the hysteresis loss can be given in watts per unit volume. An empirical relationship developed by Charles P. Steinmetz gives the hysteresis loss as;
${{P}_{h}}={{k}_{h}}fB_{m}^{n}$
Where Ph is the watts per unit volume, kh a constant term, f the number of magnetization cycles per second, Bm the maximum flux density, and n the Steinmetz constant normally taken as 1.6. It follows that the greater the energy required to magnetize a sample, the greater the energy needed to demagnetize it. Large hysteresis loops are, therefore, required for permanent magnets, because the large hysteresis loop represents a large storage of energy.
- You May Also Read: Hysteresis Loop Explained in Detail with Diagram
Eddy Current Loss
A changing magnetic field induces an emf in a conducting material in that field. Such emf, within a magnetic core, create circulating or eddy currents. The eddy currents encounter the electrical resistance of the core producing power loss proportional to I2R losses. Although the eddy current values cannot be determined directly, the power loss has been found to be given by empirically,
${{P}_{e}}={{k}_{e}}{{f}^{2}}B_{m}^{2}$
Where Pe is the eddy current loss in watts per unit volume and ke a constant; f and Bm are as previously defined. In order to reduce the magnitude of eddy currents and hence reduce the power loss in a core, magnetic cores are constructed by stacking thin laminations as shown in the following figure.
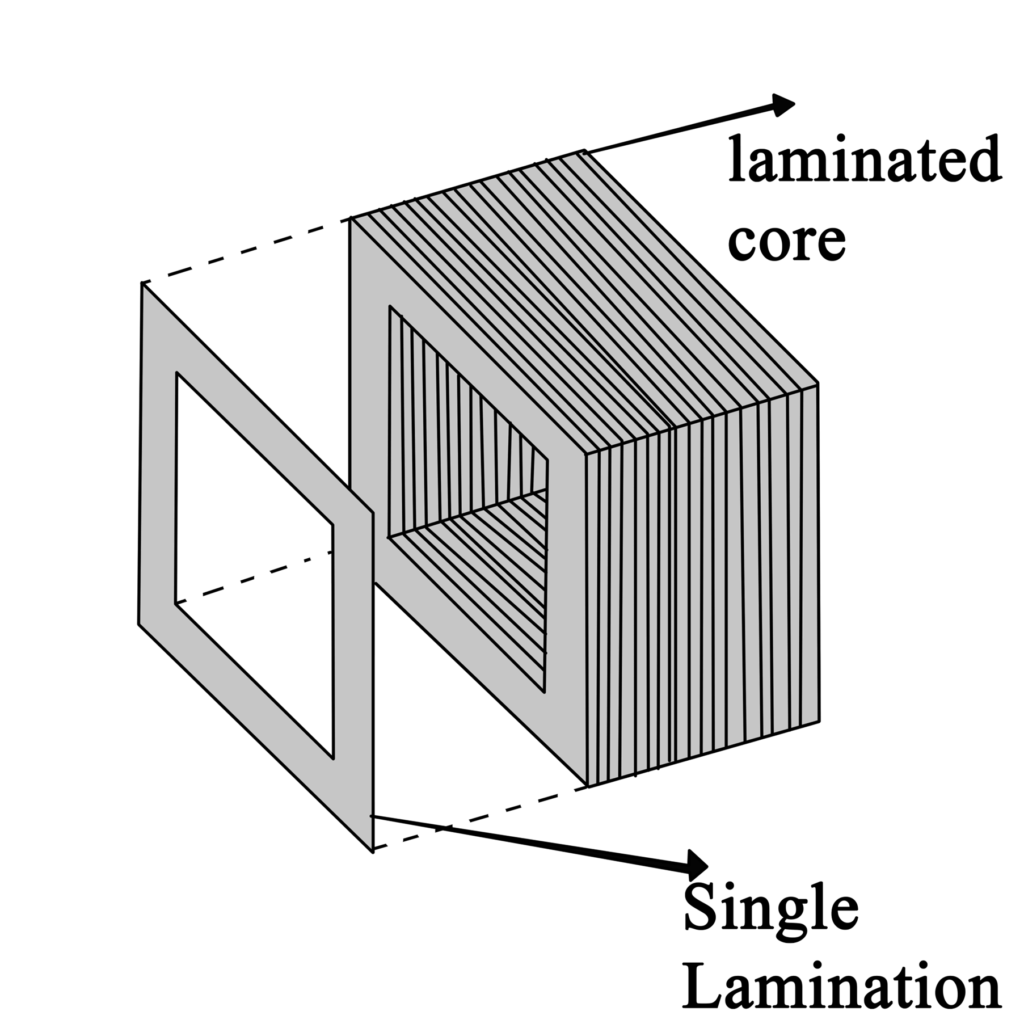
The laminations are insulated from each other by a thin coat of varnish.
In conclusion, the combined hysteresis and eddy current loss are known as the core losses.