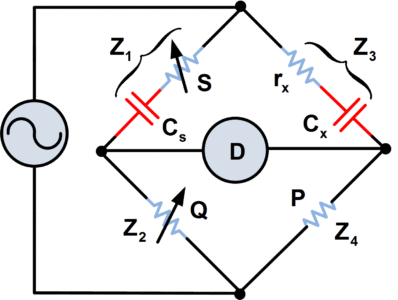
One disadvantage of simple Capacitance Bridge is that perfect balance of the bridge is obtained only when Cs and Cx are both pure capacitances (i.e. they have virtually no resistive components). In general, this occurs only with capacitors that have air or mica dielectrics. Capacitors with other types of dielectric have a leakage current, and consequently, the equivalent circuits for the capacitors have resistive components that must be included in the bridge circuit.
The circuit of the series resistance-capacitance bridge shown in figure 1 eliminates the balance problems that can occur with the simple capacitance bridge. Resistance rx in series with the unknown capacitance represents the resistive component of the capacitor equivalent circuit. The standard capacitor Cs normally has mica dielectric and thus has a very small resistive component. Consequently, the adjustable resistance S must be included in the circuit to balance the effect of rx.
- You May Also Read: Capacitance Bridge Working Principle
Working Princple of Series Resistance Capacitance Bridge
The balance equations for the series resistance capacitance bridge are derived as follows:
\[\frac{{{Z}_{1}}}{{{Z}_{2}}}=\frac{{{Z}_{3}}}{{{Z}_{4}}}\]
Therefore,
\[\frac{S-j\frac{1}{\omega {{C}_{s}}}}{Q}=\frac{{{r}_{x}}-j\frac{1}{\omega {{C}_{x}}}}{P}\]
\[\begin{matrix} \frac{S}{Q}-j\frac{1}{\omega {{C}_{s}}Q}=\frac{{{r}_{x}}}{P}-j\frac{1}{\omega {{C}_{x}}P} & \cdots & (1) \\\end{matrix}\]
For equation (1) to be correct, the real parts on each side must be equal, and the imaginary parts on each side must be equal.
Equating the real parts,
\[\frac{S}{Q}=\frac{{{r}_{x}}}{P}\]
And
[stextbox id=”info” caption=”Resistive Component of the Unknown Capacitance”]\[\begin{matrix} {{r}_{x}}=\frac{PS}{Q} & \cdots & (2) \\\end{matrix}\][/stextbox]
Fig.1: Series Resistance Capacitance Bridge
The use of series resistors with a capacitance bridge makes balance easy to obtain and allows the resistive component of the capacitors to be measured.
Now, equating the imaginary parts,
\[\frac{1}{\omega {{C}_{s}}Q}=\frac{1}{\omega {{C}_{x}}P}\]
And
[stextbox id=”info” caption=”Formula for Unknown Capacitance”]\[\begin{matrix} {{C}_{x}}=\frac{Q{{C}_{s}}}{P} & \cdots & (3) \\\end{matrix}\][/stextbox]
The resistive and capacitive components of the unknown capacitance can now be calculated by means of equations (2) and (3). Note that neither the supply voltage nor the AC frequency is involved in the balance equations for the bridge.
Because of the need to balance the real and imaginary components of the bridge impedances, the process of obtaining balance in an AC bridge is a little more complicated than with the Wheatstone bridge. One of the adjustable components (Q or S in figure 1) is first altered to obtain the lowest possible indication of the null meter. Then the other adjustable component is varied to obtain the lowest reading. The process is repeated until further adjustment of either component cannot produce a lower reading on the null meter. At this point the bridge is balanced.
- You May Also Read: Maxwell Inductance Bridge Working Principle