Laplace Transform Definition
The Laplace transform X(s) is a complex-valued function of the complex variable s. In other words, given a complex number s, the value X(s) of the transform at the point s is, in general, a complex number.
Given a function x (t) of the continuous-time variable t, the two-sided Laplace transform of x (t), denoted by X(s), is a function of the complex variable s=σ+jω defined by
\[X(s)=\int_{-\infty }^{\infty }{x(t){{e}^{-st}}dt}\text{ }(1)\]
The one-sided Laplace transform of x (t), also denoted by X(s), is defined by
\[X(s)=\int_{0}^{\infty }{x(t){{e}^{-st}}dt}\text{ (2)}\]
By (2), we see that one-sided transform depends only on the values of the signal x (t) for t≥0. This is the reason that definition (2) of the transform is called the one-sided Laplace transform. We can apply the one-sided Laplace transform to signals x (t) that are nonzero for t<0; however, any nonzero values of x (t) for t<0 will not be recomputable from the one-sided transform.
- You May Also Read: Laplace Transform Properties
If x (t) is zero for all t<0, the expression (1) reduces to (2), and thus, in this case, the one-sided and two-sided transforms are the same. Let Λ denote the set of all positive or negative real numbers σ such that
\[X(s)=\int_{0}^{\infty }{\left| x(t) \right|{{e}^{-\sigma t}}dt}<\infty \text{ (3)}\]
If the set Λ is empty, that is, there is no real number σ such that (3) is satisfied, the function x (t) does not have a Laplace transform (which converges “absolutely”). Most functions arising in engineering do have a Laplace transform, and thus the set Λ is not empty in many cases of interest.
If Λ is not empty, let σmin denote the minimal element of the set Λ; that is, σmin is the smallest number such that
σϵ Λ for all σ> σmin
The set of all complex numbers s such that
\[Real\text{ }s>{{\sigma }_{min}}\text{ (4)}\]
Where Real s = real part of s, is called the region of absolute convergence of the Laplace transform of x (t). for any complex number s such that (4) is satisfied, the integral in (2) exists, and thus the Laplace transform X(s) exists for this values of s. Hence the Laplace transform X (s) of x (t) is well defined for all values of s belonging to the region of absolute convergence. It should be stressed that the region of absolute convergence depends on the given function x (t).
Laplace Transform Example
Suppose that x (t) is the unit step function u(t). then the Laplace transform U (s) of u (t) is given by
\[U(s)=\int\limits_{0}^{\infty }{u(t){{e}^{-st}}dt}\]
\[=\int\limits_{0}^{\infty }{{{e}^{-st}}dt}\]
\[=-\frac{1}{s}\left. {{e}^{-st}} \right]_{t=0}^{t=\infty }\text{ (5)}\]
Now exp (-st) evaluated at t=∞ is defined by
\[{{e}^{-s\infty }}=\underset{T\to \infty }{\mathop{\lim }}\,{{e}^{-sT}}\text{ (6)}\]
Setting s=σ+jω in the right side of (6), we have
\[{{e}^{-s\infty }}=\underset{T\to \infty }{\mathop{\lim }}\,[-(\sigma +j\omega )T]\]
\[=\underset{T\to \infty }{\mathop{\lim }}\,{{e}^{-\sigma T}}{{e}^{-j\omega T}}\text{ (7)}\]
The limit in (7) exists if and only if σ>0, which is equivalent to Real s >0. If Real s>0, the limit in (7) is zero, and the expression (5) for U (s) reduces to
$U(s)=-(-\frac{1}{s}){{e}^{0}}=\frac{1}{s}$
We also have
\[\int\limits_{0}^{\infty }{u(t){{e}^{-\sigma t}}dt<\infty }\]
For all real numbers σ such that σ>0. Thus the region of absolute convergence of U (s) is the set of all complex numbers s such that Real s >0.
Little Explanation
The limit in (7) exists if and only if σ>0. WHY?
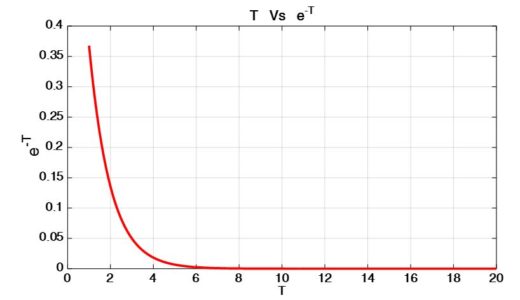
Let’s take a look at this issue by plotting the given function
\[{{e}^{-s\infty }}=\underset{T\to \infty }{\mathop{\lim }}\,{{e}^{-\sigma T}}\]
Since we are just dealing with real part (σ) of s, so we intentionally ignored e-jwT . In order to plot the above function, we assume σ=1 (it could be any number > 0).
Matlab Code:
T=[1:0.1:20];
y=exp(-T);
plot(T,y)
Graph:
So, if we look at the graph, we can perceive that the function clearly approaches 0 as T→∞. Hence, If Real s>0, the limit in (7) is zero.
Very Informative and to the point.Great write up.