If we connect a capacitor across a sine-wave voltage source, as in Figure 1, Kirchhoff’s voltage law requires the voltage across the capacitor to be exactly the same as the applied voltage at every instant.
The voltage across a capacitor can change only if the capacitor charges or discharges. Consequently, the capacitor in Figure 1 must charge and discharge in such a manner that the voltage across it is a sine wave equal to the applied voltage at every instant. Since q = Cv,
\[\frac{dq}{dt}=C\frac{dv}{dt}\]
By definition, $i=\frac{dq}{dt}$. Therefore,
\[\begin{matrix}i=C\frac{dv}{dt} & {} & \left( 1 \right) \\\end{matrix}\]
Since capacitance depends on such physical factors as the area of the plates and the dielectric constant of the material between the plates, the capacitance of a given circuit does not depend on the elapsed time. Since we can treat C in Equation 1 as a constant, this equation shows that the instantaneous current in Figure 1 is directly proportional to the rate at which the voltage across the capacitor is changing.
Figure 1 Capacitance in an alternating-current circuit
The blue sine curve in Figure 2 represents the instantaneous voltage across the capacitor. This curve shows that the maximum voltage across the capacitor occurs π/2 radians after the maximum rate of change of voltage. At the exact moment when the voltage across the capacitor is greatest, the voltage is neither rising nor falling. Therefore, the instantaneous current must be zero at this instant.
The maximum rate of change of voltage occurs when the voltage sine curve is steepest. At this instant the voltage is zero, indicating that the capacitor has just finished discharging its stored charge and is about to start building up an opposite charge. Therefore, the instantaneous current has its maximum positive value at the instant when the voltage across the capacitor changes from a negative polarity to a positive polarity.
Similarly, the current reaches its maximum negative value just as the voltage changes from a positive to a negative polarity.
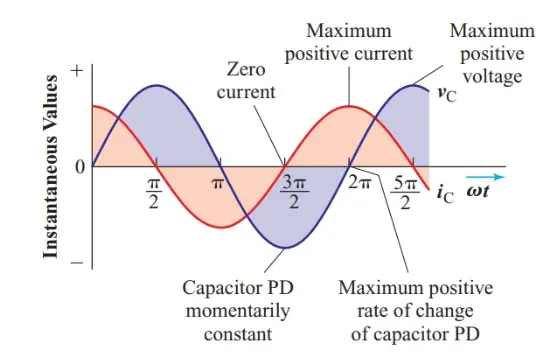
Figure 2 Instantaneous current in a capacitor
The instantaneous current must have the sine-wave shape shown by the red curve in Figure 2 in order for the voltage across the capacitor to match the applied voltage at every instant.
The instantaneous current is at its maximum positive value at the instant that the voltage across the capacitor is just starting to increase from zero. When the voltage across the capacitance has reached its positive peak π/2 rad later, the instantaneous current has fallen back to zero. Therefore,
For a sine-wave voltage to be developed across a capacitor, the current through it must be a sine wave that leads the instantaneous voltage by π/2 radians.
Therefore, the instantaneous current in the circuit of Figure 1 is
\[\begin{matrix}{{i}_{c}}={{\operatorname{I}}_{m}}\sin \left( \omega t+\frac{\pi }{2} \right) & {} & \left( 2 \right) \\\end{matrix}\]
Where the phase angle ωt + π /2 is measured in radians.
You May Also Read: Instantaneous Current in an Ideal Inductor