Block Diagram in Contol System
By using block diagrams when examining larger systems, attention can be focused on a smaller number of elements or subsystems whose properties may already be known. By doing this, a set of individual blocks representing the various elements or subsystems is formed, and these blocks are interconnected to represent the whole system. Each block represents the transfer function of a particular subsystem or element, and the function and performance of the whole system can be analyzed by studying the effect of the interconnections. The interconnected blocks then visually represent the differential equations of the control system. In some situations, the blocks are just constants representing the gains of a system, such as amplification, scaling or generator constants.
Thus, the block diagram serves as an organizational and visual aid that can be reduced and simplified for a linear system. When separating a larger system into smaller subsystems or components, it is necessary to select interface boundaries so that the loading effect of adjacent systems do not change the characteristics or the transfer function of a particular element being modeled. Some common elements in a block diagram are given below.
- You May Also Read: Feedback Control System Advantages and Disadvantages
Single Blocks
A system or element whose transfer function is G(s) may be represented by a block diagram, as shown in the figure.
Fig.1: Block diagram of transfer function G(s)
If the transfer function is a constant K, the diagram in the following figure is used.
Fig.2: Block diagram of constant K
These blocks represented the algebraic equations:
$Y(s)=G(s)X(s)$
And
$Y(s)=KX(s)$
At times the value of the transfer function is displayed in the block, as shown in the following figure, for first order system.
Fig.3: First-Order System
The blocks in the following figures represent scaled integration and differentiation.
Fig.4: Integration
Fig.5: Differentiation
Cascaded Blocks
The output of the block is frequently the input of another block, as shown in figure:
Fig.6: Individual systems
The second block must not alter the performance of the first block; in effect, then, the second block must offer a reasonably high input impendence. If the interaction of blocks causes a change in the individual transfer functions, we must perform an analysis to combine the blocks into one before using them in the diagram.
As shown in the following figure, cascaded elements can be combined into one block in accordance with block diagram algebra as
Fig.7: Combined systems
$\frac{Z(s)}{X(s)}=\left[ \frac{Y(s)}{X(s)} \right]\left[ \frac{Z(s)}{Y(s)} \right]={{G}_{1}}(s){{G}_{2}}(s)$
For linear systems, the individual blocks commute, that is
${{G}_{1}}(s){{G}_{2}}(s)={{G}_{2}}(s){{G}_{1}}(s)$
By extension, any number of cascaded blocks can be combined into a single block by multiplying the transfer functions.
Comparator and Summing Point
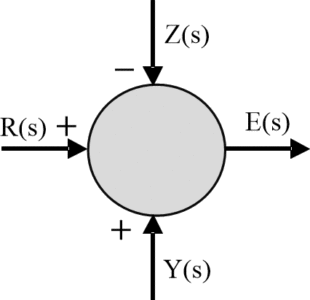
In the s-domain, the following diagram represents a summer to express the function:
$e(t)=r(t)+y(t)-z(t)$
Fig.8: Summer
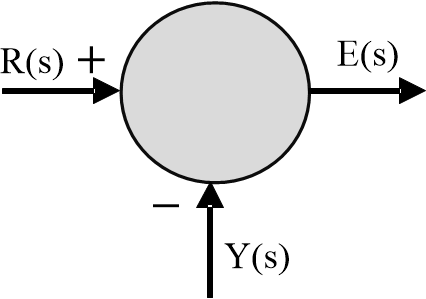
Similarly, the device of the following figure is used to express the function
$e(t)=r(t)-y(t)$
Fig.9: Comparator
And is called a comparator; it is a special case of a summer.
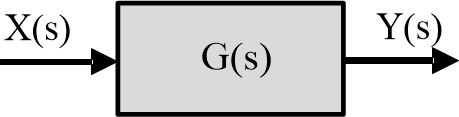

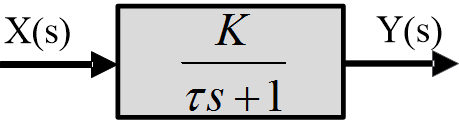
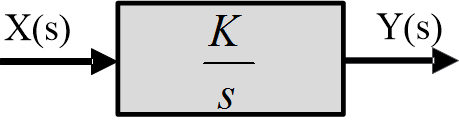
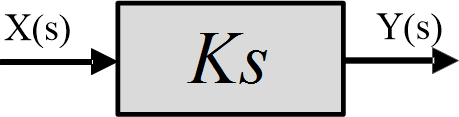

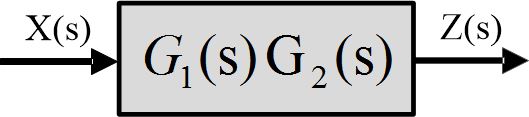
Somebody essentially assist to make significantly articles I might state. That is the first time I frequented your website page and up to now? I amazed with the research you made to create this actual submit amazing. Great process!