Although the sine wave is by far the most important AC waveform, there are many other types of periodic waves.
In electric circuits, a periodic wave is any time-varying quantity, such as voltage, current, or power that continually repeats exactly the same sequence of values with each cycle taking exactly the same time.
Periodic Wave Examples
Figure 1 shows how the instantaneous values of six common periodic waves vary as a function of time. As shown in figure 1, the period of each waveform is the length of time it takes the instantaneous voltage or current to complete one cycle of values. Figure 1(b) shows four complete cycles of a periodic wave. All other graphs in figure 1 show two complete cycles.
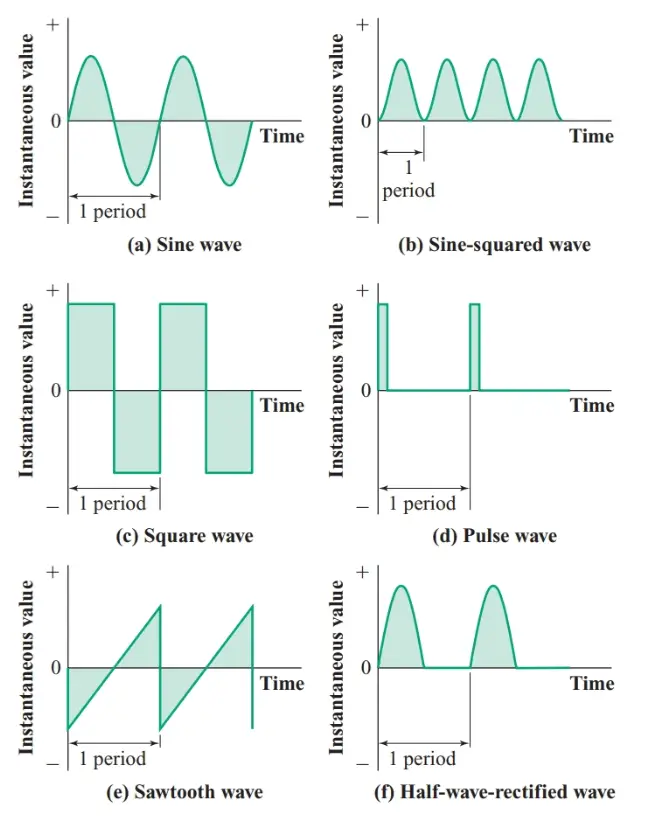
Figure 1 Some common periodic waves
The instantaneous values of a periodic wave change much too rapidly to be registered by a conventional electric meter. However, a cathode-ray tube or a liquid crystal display (LCD) in an oscilloscope can quite readily respond to high-frequency instantaneous voltages.
If the instantaneous voltage of a certain periodic wave, such as the sine wave of figure 1(a), is applied to the vertical deflection circuit of an oscilloscope, the display will show a dot of light moving up and down exactly in step with the voltage. For most waves, this motion is still much too rapid for the eye to follow, so what we see is a vertical line with a length proportional to the peak-to-peak value of the voltage of the periodic wave.
In the sawtooth periodic wave of figure 1(e), the instantaneous voltage is a linear function of elapsed time. Hence, if the horizontal deflection circuit of the oscilloscope generates a sawtooth wave having a period exactly twice that of the waveform fed to the vertical deflection circuit, the screen will display two cycles of that waveform. Multi-trace oscilloscopes can display two or more waveforms at the same time.
Average Value of a Periodic Wave
By definition, an alternating current or voltage is one in which the arithmetic average, or mean, of the instantaneous values over a cycle is zero.
From an examination of figure 1, it is fairly obvious that the sine, square, and sawtooth waveforms are alternating because the instantaneous values are symmetrical about the horizontal axis of the graph. The sine-squared wave, pulse wave, and half-wave-rectified wave are not alternating currents because their instantaneous values always have the same polarity.
For complex periodic waves, we can determine the mean of the instantaneous values graphically by examining the area under a graph.
Since the sine wave is symmetrical, each positive value during the first half-cycle has a matching negative value during the next half-cycle. Therefore, the mean value of a complete cycle of a sine wave is zero, and the mean value of the first half-cycle is equal in magnitude but opposite in polarity to the mean of the second half-cycle.
Since i = Im sinωt, the half-cycle average value of a sinusoidal current is
$\begin{matrix}{{I}_{av}}=\frac{2}{\pi }{{\operatorname{I}}_{m}}\approx 0.637{{\operatorname{I}}_{m}} & {} & \left( 1 \right) \\\end{matrix}$
Similarly, the half-cycle average value of a sinusoidal source voltage is
$\begin{matrix}{{E}_{av}}=0.637{{E}_{m}}=\frac{2}{\pi }{{E}_{m}} & {} & \left( 2 \right) \\\end{matrix}$
- The sine-squared wave of figure 1(b) has a full-cycle average value of one-half the peak value of the sine-squared wave.
- The pulse waveform of figure 1(d) has an average value that depends on the ratio of the pulse duration to the period of the wave.
- The full-cycle average value of the half-wave-rectified wave of figure 1(f) is the mean of 0.637Em for one half-cycle and zero for the next half-cycle, or 0.3183Em.