All electric circuits convert electric energy into some other form of energy, such as heat, light, or mechanical energy. For many of these energy conversions, it does not matter whether the energy source for the circuit produces direct current or alternating current. Therefore, we find equivalent steady-state values for alternating current and voltage that allow us to use the same relationships among voltage, current, resistance, power, work, and so on, that we use for DC circuits.
We can determine an equivalent DC value or effective value of an alternating current experimentally by finding the direct current that produces heat in a given resistance at the same rate as when the resistance is connected to a source of alternating voltage. We can also use algebraic analysis to find such equivalent values.
To determine the equivalent DC value of an alternating current, we first find the average power in a resistive AC circuit. Since$p={{i}^{2}}R$,
${{P}_{av}}=\left( full-cycle\text{ }average\text{ }of\text{ }{{i}^{2}} \right)\times R$
In a DC circuit, P = I2R. Since the effective values of an alternating current are to represent DC equivalent values, we can use the same letter symbols for both, that is, uppercase italic letters without subscripts. Therefore, in an AC circuit,
$P={{I}^{2}}R$
Where P is average power and I is the DC equivalent for the alternating current. Solving for I gives
$\begin{align}& I=\sqrt{\frac{P}{R}}=\sqrt{\frac{\left( full-cycle\text{ }average\text{ }of\text{ }{{i}^{2}} \right)\times R}{R}} \\& =\sqrt{full-cycle\text{ }average\text{ }of\text{ }{{i}^{2}}} \\\end{align}$
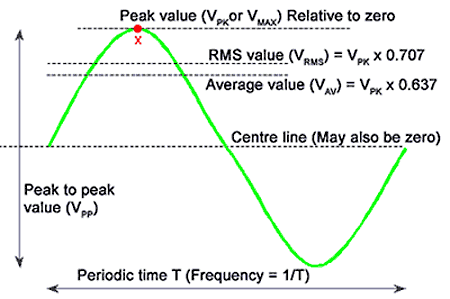
Thus I is equal to the square root of the mean of the squares of the instantaneous current over a full cycle. Root-mean-square (RMS) value, effective value, and equivalent DC value all mean the same thing. For the rest of the section, we use the term RMS.
Figure 1 shows that the instantaneous power for a sine wave of alternating current swings alternately and symmetrically between zero and peak power. Therefore, the average power in a resistor through which a sine-wave alternating current is flowing is simply one-half the peak power.
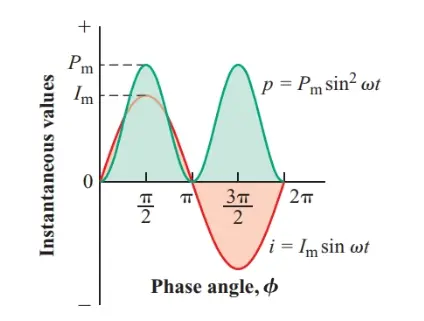
Figure 1 Instantaneous power in a resistor
We can also determine this relationship from the general equation for instantaneous power:
$\begin{matrix}p={{P}_{m}}{{\sin }^{2}}\omega t & {} & \left( a \right) \\\end{matrix}$
Where
${{\sin }^{2}}\omega t=\frac{1}{2}\left( 1-\cos 2\omega t \right)$
If we average a sine or cosine function over a complete cycle, the average must be zero, since for every positive value during the first half-cycle, there is a matching equivalent negative value during the second half-cycle. Hence, when averaged over a complete cycle, Equation a becomes
$\begin{matrix}P=\frac{1}{2}{{P}_{m}} & {} & \left( 1 \right) \\\end{matrix}$
For a sine-wave alternating current in an AC circuit,
$\begin{matrix}P={{I}^{2}}R & and & {{P}_{m}}=I_{m}^{2}R \\\end{matrix}$
But
$P=\frac{1}{2}{{P}_{m}}=\frac{1}{2}I_{m}^{2}R$
Therefore,
\[\begin{align}& {{I}^{2}}R=\frac{1}{2}I_{m}^{2}R \\& \begin{matrix}I=\frac{{{\operatorname{I}}_{m}}}{\sqrt{2}}\approx 0.707{{\operatorname{I}}_{m}} & {} & \left( 2 \right) \\\end{matrix} \\\end{align}\]
The RMS (effective) value of a sine wave of current is ${}^{1}/{}_{\sqrt{2}}$ , or about 0.707, times the peak value.
The RMS value of a sine-wave voltage should be such that the average power is the product of the RMS voltage across and RMS current through the resistance of the circuit, just as P = VI in the equivalent DC circuit.
Since peak instantaneous power occurs at the instant when both the voltage across and the current through a resistance circuit reach their peak values,
${{P}_{m}}={{V}_{m}}{{\operatorname{I}}_{m}}$
Substituting into equation 1 gives
\[P=VI=V\frac{{{\operatorname{I}}_{m}}}{\sqrt{2}}=\frac{1}{2}{{P}_{m}}=\frac{1}{2}{{V}_{m}}{{\operatorname{I}}_{m}}\]
Therefore,
\[\begin{matrix}V=\frac{{{V}_{m}}}{\sqrt{2}}\approx 0.707{{V}_{m}} & {} & \left( 3 \right) \\\end{matrix}\]
And
\[{{V}_{m}}=\sqrt{2}V\approx 1.414V\]
Example 1
Find the peak voltage of a 120-V 60-Hz electric service.
Solution
${{E}_{m}}=1.414E=1.414\times 120V=170V$
Form Factor
A term we may encounter occasionally when working with AC waveforms is form factor. Form factor is the ratio of the RMS value to the half- cycle average value of an AC wave. For a sine wave,
\[\begin{matrix}Form-Factor=\frac{I}{{{I}_{av}}}\approx \frac{0.707{{\operatorname{I}}_{m}}}{0.637{{\operatorname{I}}_{m}}}=1.11 & {} & \left( 4 \right) \\\end{matrix}\]
- You May Also Read: Average Power Formula | Instantaneous Power Formula