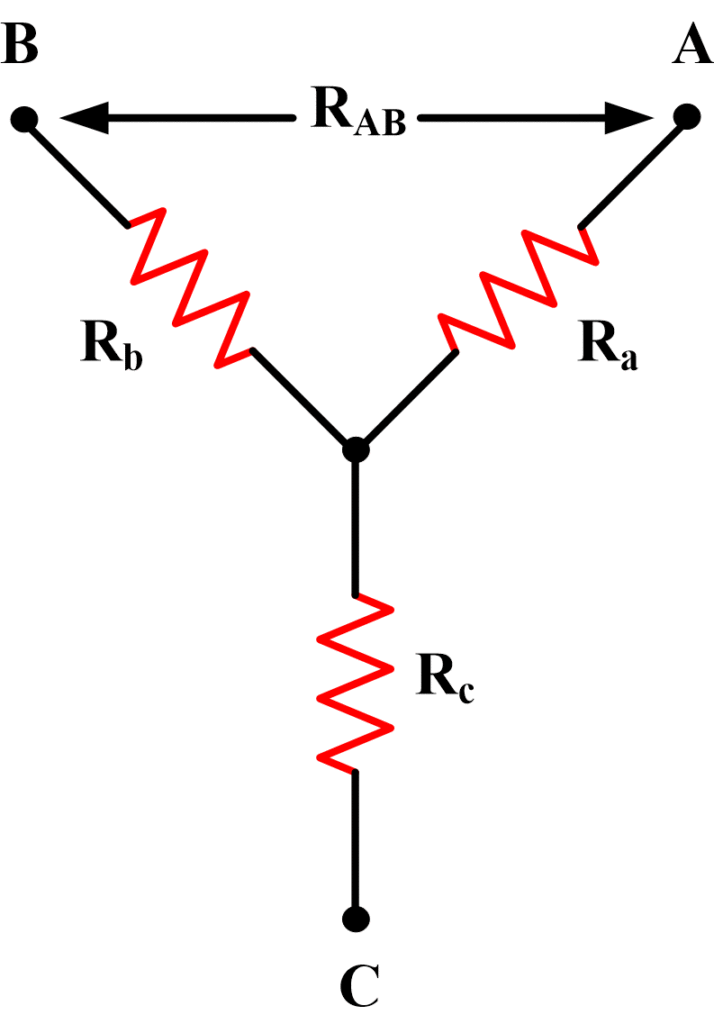
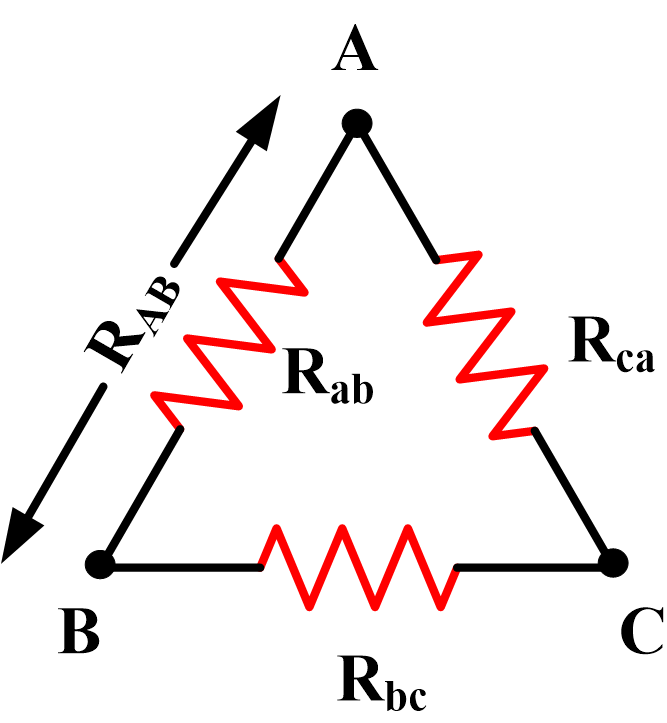
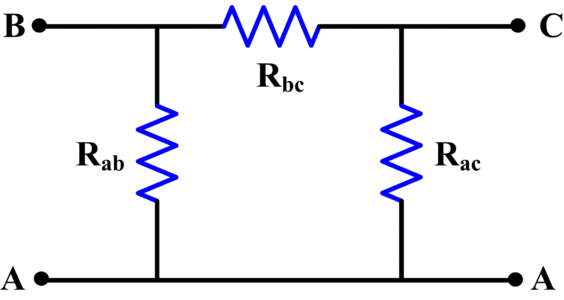
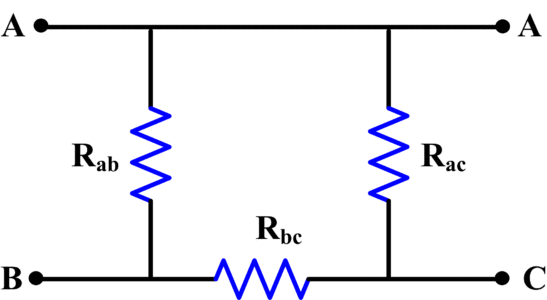
Wye (Star) and Delta networks identified for conversion in converting between types. In the Wye (Star) networks, each resistor is named for the terminal it is connected to: Ra, Rb, and Rc. For the Delta (Pie) networks, each resistor is named for the two terminals it is connected across: Rab, Rbc, and Rca.
Sometimes, in an electric circuit, resistors are connected either in Wye (or Star) form or Delta (or Pie) form. In such situations, we want to determine the relationships between the resistances that allow us to transform a given Delta network into an equivalent Wye (Y) network, or vice versa.
Fig.1: Wye (Y) Network
Fig.2: Delta Network
In order to convert wye circuit into Delta one or vice versa, a set of equations is used.
Delta to Wye Transformation
Wye circuit is commonly known as star circuit. In order to convert delta connected resistors to wye network, we use following a set of equations:
\[\begin{matrix} {{R}_{a}}=\frac{{{R}_{ab}}{{R}_{ac}}}{{{R}_{ab}}+{{R}_{ac}}+{{R}_{bc}}} & {} & \left( 1 \right) \\\end{matrix}\]
\[\begin{matrix} {{R}_{b}}=\frac{{{R}_{ab}}{{R}_{bc}}}{{{R}_{ab}}+{{R}_{ac}}+{{R}_{bc}}} & {} & \left( 2 \right) \\\end{matrix}\]
\[\begin{matrix} {{R}_{c}}=\frac{{{R}_{ac}}{{R}_{bc}}}{{{R}_{ab}}+{{R}_{ac}}+{{R}_{bc}}} & {} & \left( 3 \right) \\\end{matrix}\]
The subscripts used in above equations can be seen in above network figures.
Equations 1, 2, and 3 can be used to convert from Delta to Wye (Y). examination of equation 1 shows that to obtain the Y network resistor Ra connected to terminal A, the two Delta connected resistors connected to A must be multiplied together, and the product divided by the sum of the three Delta network resistors. A similar procedure applies for obtaining the Y network resistors connected to terminal B and C.
Wye to Delta Transformation
In this case, to convert wye connected resistors to Delta connection, following a set of equations can be used:
\[\begin{matrix} {{R}_{ab}}=\frac{{{R}_{a}}{{R}_{b}}+{{R}_{a}}{{R}_{c}}+{{R}_{b}}{{R}_{c}}}{{{R}_{c}}} & {} & \left( 4 \right) \\\end{matrix}\]
\[\begin{matrix} {{R}_{ac}}=\frac{{{R}_{a}}{{R}_{b}}+{{R}_{a}}{{R}_{c}}+{{R}_{b}}{{R}_{c}}}{{{R}_{b}}} & {} & \left( 5 \right) \\\end{matrix}\]
\[\begin{matrix} {{R}_{bc}}=\frac{{{R}_{a}}{{R}_{b}}+{{R}_{a}}{{R}_{c}}+{{R}_{b}}{{R}_{c}}}{{{R}_{a}}} & {} & \left( 6 \right) \\\end{matrix}\]
Once again, examination of the three equations reveals a definite pattern. To obtain the Delta resistor connected between any two terminals, divide the Y resistor connected to the terminal opposite those two (terminal C for the resistor between A and B) into the sum of the products of each pair of Y resistors.
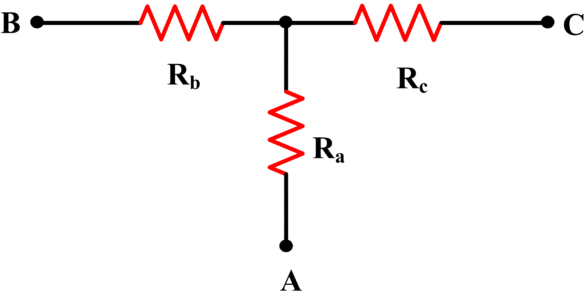
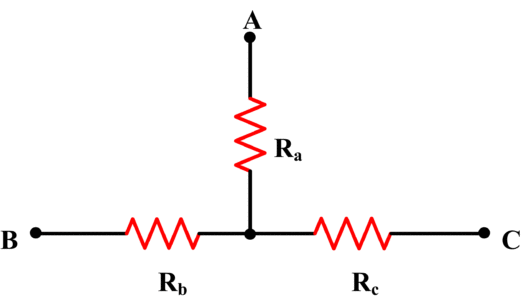
The Y network is also known as a star network or a T network. Figures 3 and 4 show Y networks redrawn in a slightly different form.
Fig.3: Y-Network (T-Form)
Fig. 4: Y-Network (T-Form)
Delta networks are also termed mesh or pi networks. Figure 5 and 6 show delta networks are redrawn in a different form.
Fig.5: Delta Network (Pi Form)
Fig.6: Delta Network (Pi Form)
Special Case
Sometimes, we encounter a situation where all wye connected resistors are equal and similarly Delta connected resistors are equal such as:
${{R}_{a}}={{R}_{b}}={{R}_{c}}={{R}_{Y}}$
And
${{R}_{ab}}={{R}_{bc}}={{R}_{ac}}={{R}_{\Delta }}$
In this particular case, the transformation is quite easier and can be done using the simple relation between wye connected and delta connected resistors.
${{R}_{\Delta }}=3{{R}_{Y}}$
Using above equation, wye to delta and delta to wye transformation can be done with signification ease.
Delta-Wye and Wye-Delta Transformation Procedure
Step 1:
When starting with a Delta network, draw a Y network.
When starting with a Y network, draw a Delta network.
Step 2:
Identify the three corresponding terminals on each network as A, B, and C.
Step 3:
(a). Identify the resistors on the Delta network:
Resistor between terminals A and B as Rab
Resistor between terminals A and C as Rac
Resistor between terminals B and C as Rbc
(b). Identify the resistors on the Y network:
Resistor connected to terminal A as Ra
Resistor connected to terminal B as Rb
Resistor connected to terminal C as Rc
Step 4:
(a). For Delta to Y transformation, substitute the Delta network resistor values into equations 1, 2, and 3 to obtain the Y network resistor values.
(b). For Y to Delta transformation, substitute the Y network resistor values into equations 4, 5, and 6 to obtain the Delta network resistor values.
Example of Delta to Wye (Star) transformation
Convert the Delta connected resistors shown in figure 2 above to a Y network. Then convert back again to prove the formula. Take Rab=500Ω, Rac=400Ω, and Rbc=300Ω.
Solution
For Delta to Y network conversion:
Equation 1,
\[\begin{align} & {{R}_{a}}=\frac{{{R}_{ab}}{{R}_{ac}}}{{{R}_{ab}}+{{R}_{ac}}+{{R}_{bc}}} \\ & =\frac{500\times 400}{500+400+300}=166.7\Omega \\\end{align}\]
Equation 2,
\[\begin{align} & {{R}_{b}}=\frac{{{R}_{ab}}{{R}_{bc}}}{{{R}_{ab}}+{{R}_{ac}}+{{R}_{bc}}} \\ & =\frac{500\times 300}{500+400+300}=125\Omega \\\end{align}\]
Equation 3,
$\begin{align} & {{R}_{c}}=\frac{{{R}_{ac}}{{R}_{bc}}}{{{R}_{ab}}+{{R}_{ac}}+{{R}_{bc}}} \\ & =\frac{400\times 300}{500+400+300}=100\Omega \\\end{align}$
Converting back from Y to Delta:
Equation 4,
\[\begin{align} & {{R}_{ab}}=\frac{{{R}_{a}}{{R}_{b}}+{{R}_{a}}{{R}_{c}}+{{R}_{b}}{{R}_{c}}}{{{R}_{c}}} \\ & =\frac{\left( 166.7\times 125 \right)+\left( 166.7\times 100 \right)+\left( 125\times 100 \right)}{100}=500\Omega \\\end{align}\]
Equation 5,
$\begin{align} & {{R}_{ac}}=\frac{{{R}_{a}}{{R}_{b}}+{{R}_{a}}{{R}_{c}}+{{R}_{b}}{{R}_{c}}}{{{R}_{b}}} \\ & =\frac{\left( 166.7\times 125 \right)+\left( 166.7\times 100 \right)+\left( 125\times 100 \right)}{125}=400\Omega \\\end{align}$
Equation 6,
$\begin{align} & {{R}_{bc}}=\frac{{{R}_{a}}{{R}_{b}}+{{R}_{a}}{{R}_{c}}+{{R}_{b}}{{R}_{c}}}{{{R}_{a}}} \\ & =\frac{\left( 166.7\times 125 \right)+\left( 166.7\times 100 \right)+\left( 125\times 100 \right)}{166.7}=300\Omega \\\end{align}$
Delta to Wye (Star) transformation using Matlab
Here, we will solve the same above example using Matlab code.
clear all;close all;clc
% This code is written according to Figure 1 in the text. You can change
% it in case having different Delta-Wye Configurations
%%
% Here, Insert Delta-Connection Resistance Values
R_ab=input('R_ab=');
R_bc=input('R_bc=');
R_ac=input('R_ac=');
% Output is "Star Connection Resistances" as given in the text
[R_a,R_b,R_c]=delta2star(R_ab,R_bc,R_ac);
Function delta2star.m
function[R_a,R_b,R_c]=delta2star(R_ab,R_bc,R_ac)
R_a=(R_ab*R_ac)/(R_ab+R_bc+R_ac);
R_b=(R_ab*R_bc)/(R_ab+R_bc+R_ac);
R_c=(R_ac*R_bc)/(R_ab+R_bc+R_ac);
fprintf('Delta Resistances \t Star Resistances\n ')
fprintf('R_ab=%.2f \t R_a=%.2f \n',R_ab,R_a);
fprintf('R_bc=%.2f \t R_b=%.2f \n',R_bc,R_b);
fprintf('R_ac=%.2f \t R_c=%.2f \n',R_ac,R_c);
end
Results:
Delta Resistances Star Resistances
R_ab=500 R_a=166.67
R_bc=300 R_b=125.00
R_ac=400 R_c=100.00
Star delta transformation is mainly used in bridge networks where resistors are neither in series manner nor in parallel, such as given below:
Circuit Analysis techniques such as superposition, Nodal analysis, Mesh analysis and Millions theorem are not of any help in solving such circuits. Therefore we use such transformation to convert bridge networks into a simplified form.