In single phase electric power, the double-subscript notation eliminates the need for both the polarity markings for voltages and direction arrows for currents. It is even more useful for representing voltages and currents in three-phase circuits, resulting in greater clarity and less confusion.
Voltage Phasor
The voltage phasor with double subscripts represents the voltage across the two nodes identified by the two subscripts. The voltage is positive during the half-cycle in which the node named by the first subscript is at a higher potential than the node named by the second subscript.
Current Phasor
The current phasor with the double subscripts represents the current flowing between two nodes of a circuit. The current is considered positive when it flows in the direction from the node identified by the first subscript toward the node identified by the second subscript.
Double Subscript Notation
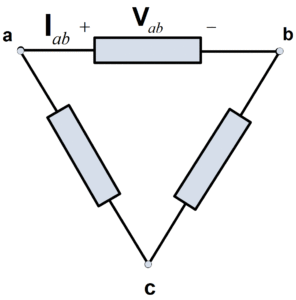
In this article, we shall find extremely useful the double subscript notation. In this case of phasors, the notation is Vab for the voltage of point a with respect to point b. we shall also use a double subscript notation for current, taking, for example, Iab as the current flowing in the direct path from point a to point b. these quantities are illustrated in figure (1), where the direct path from a to b is distinguished from the alternative path from a to b through c.
Fig.1: Illustration of Double Subscript Notation
Because of the simpler expression for average power that results, we shall use RMS values of voltage and current throughout this tutorial. That is, if
\[\begin{matrix} \text{V=}\left| \text{V} \right|\angle {{\text{0}}^{\text{o}}}\text{ V rms} & {} & {} \\ {} & {} & (1) \\ \text{I=}\left| \text{I} \right|\angle \text{- }\!\!\theta\text{ A rms} & {} & {} \\\end{matrix}\]
Are the phasors associated with an element having impedance,
$\begin{matrix} \text{Z=}\left| \text{Z} \right|\angle \text{ }\text{ }\!\!\theta\!\!\text{ }\text{ }\text{ }\Omega \text{ } & \cdots & (2) \\\end{matrix}$
The average power delivered to the element is
$\begin{matrix} P=\left| \text{V} \right|\text{.}\left| \text{I} \right|\text{cos }\theta\!\!\text{ } & {} & {} \\ {} & {} & (3) \\ ={{\left| I \right|}^{2}}\operatorname{Re}(Z)\text{ W} & {} & {} \\\end{matrix}$
In the time domain the voltage and current are
$\begin{matrix} v=\sqrt{\text{2}}\left| \text{V} \right|\text{cos }\!\!\omega\!\!\text{ t V} \\ i=\sqrt{\text{2}}\left| \text{I} \right|\text{cos( }\!\!\omega\!\!\text{ t- }\!\!\theta\!\!\text{ ) A} \\\end{matrix}$
Single Phase Voltage
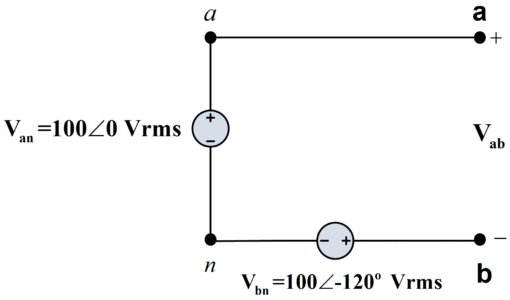
The use of double subscript makes it easier to handle phasors both analytically and geometrically. For example, in figure 2 (a), the voltage Vab is
${{\text{V}}_{\text{ab}}}\text{=}{{\text{V}}_{\text{an}}}\text{+}{{\text{V}}_{\text{nb}}}$
This is evident without referring to a circuit since by KVL the voltage between two points a and b is the same regardless of the path, which in this case is the path a,n,b. also, since Vnb=-Vbn, we have
${{\text{V}}_{\text{ab}}}\text{=}{{\text{V}}_{\text{an}}}\text{-}{{\text{V}}_{\text{bn}}}=100-100\angle -{{120}^{o}}$
Which, after simplification, is
${{\text{V}}_{\text{ab}}}=100\sqrt{3}\angle {{30}^{o}}\text{ V rms}$
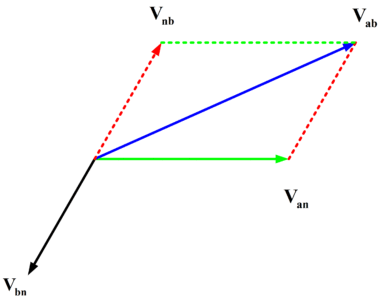
These steps are shown graphically in figure 2(b).
Fig.2: (a) Phasor Circuit
Fig.2: (b) Corresponding Phasor Diagram
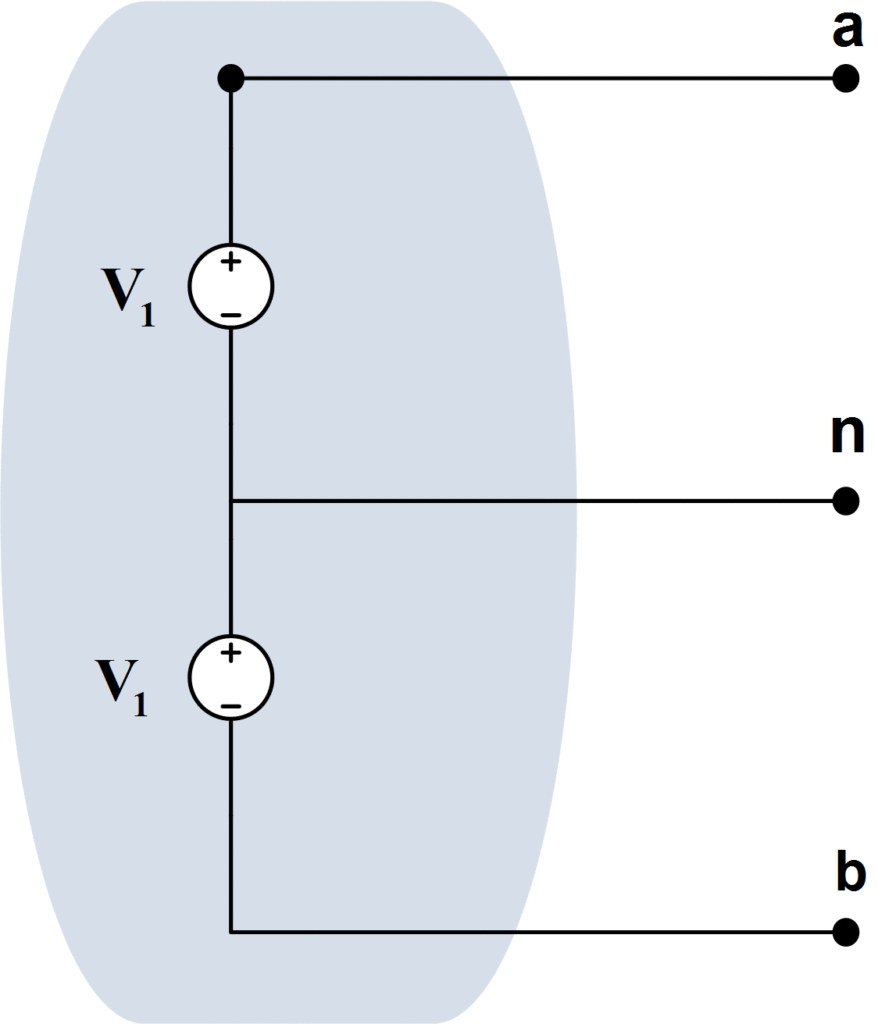
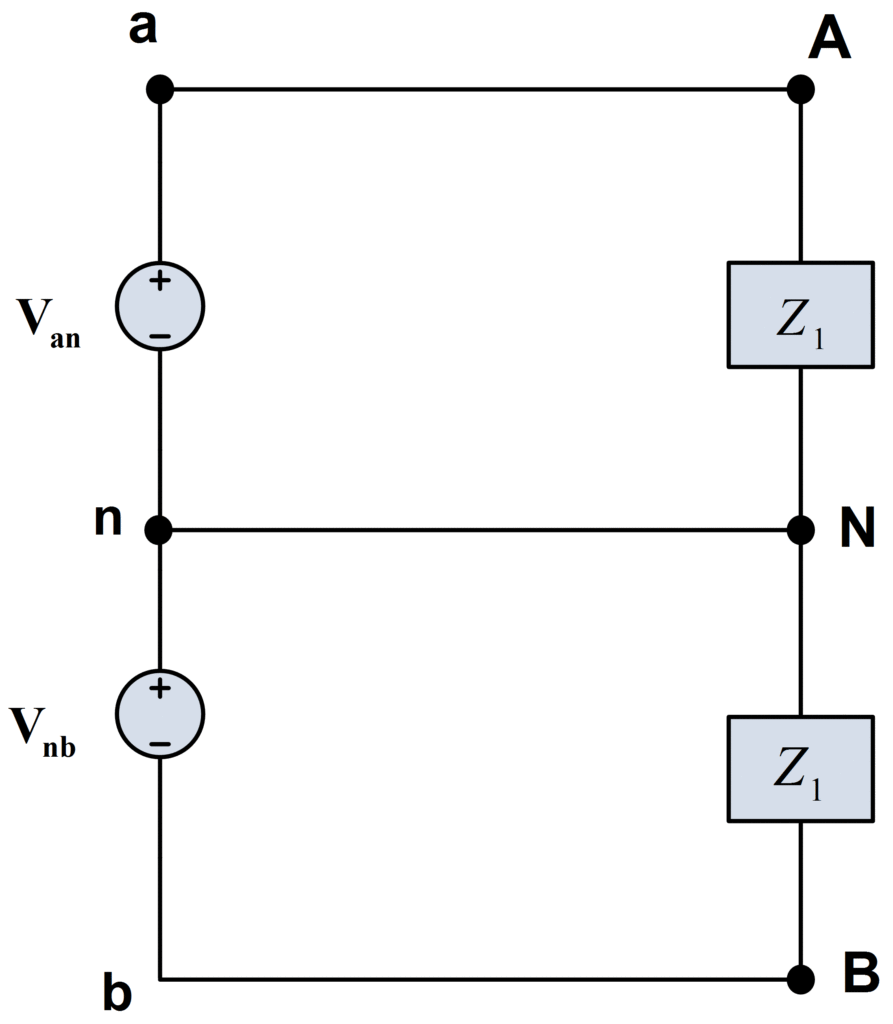
A single-phase, three-wire source, as shown in figure 3, is one having three output terminals a, b, and a neutral terminal n, for which the terminal voltages are equal. That is,
\[\begin{matrix} {{\text{V}}_{\text{an}}}\text{=}{{\text{V}}_{\text{nb}}}\text{=}{{\text{V}}_{\text{1}}} & \cdots & (4) \\\end{matrix}\]
This is a common arrangement in a normal house supplied with both 115 V and 230 V rms, since if |Van|=|V1|=115V, then |Vab|=|2V1|=230V.
Fig.3: Single-Phase, Three-Wire Source
Let us now consider the source of figure 3 loaded with two identical loads, both having an impedance Z1, as shown in figure 4.
Fig.4: Single-Phase, Three-Wire System with two Identical Loads
Single Phase Current
The currents in the lines aA and bB are
$\begin{align}& {{\text{I}}_{\text{aA}}}\text{=}\frac{{{\text{V}}_{\text{an}}}}{{{\text{Z}}_{\text{1}}}}\text{=}\frac{{{\text{V}}_{\text{1}}}}{{{\text{Z}}_{\text{1}}}} \\& \text{and} \\& {{\text{I}}_{\text{bB}}}\text{=}\frac{{{\text{V}}_{\text{bn}}}}{{{\text{Z}}_{\text{1}}}}\text{=-}\frac{{{\text{V}}_{\text{1}}}}{{{\text{Z}}_{\text{1}}}}\text{=-}{{\text{I}}_{\text{aA}}} \\\end{align}$
Therefore the current in the neutral wire, nN, by KCL is
${{\text{I}}_{\text{nN}}}\text{=-(}{{\text{I}}_{\text{aA}}}\text{+}{{\text{I}}_{\text{bB}}}\text{)=0}$
Thus the neutral could be removed without changing any current or voltage in the system.
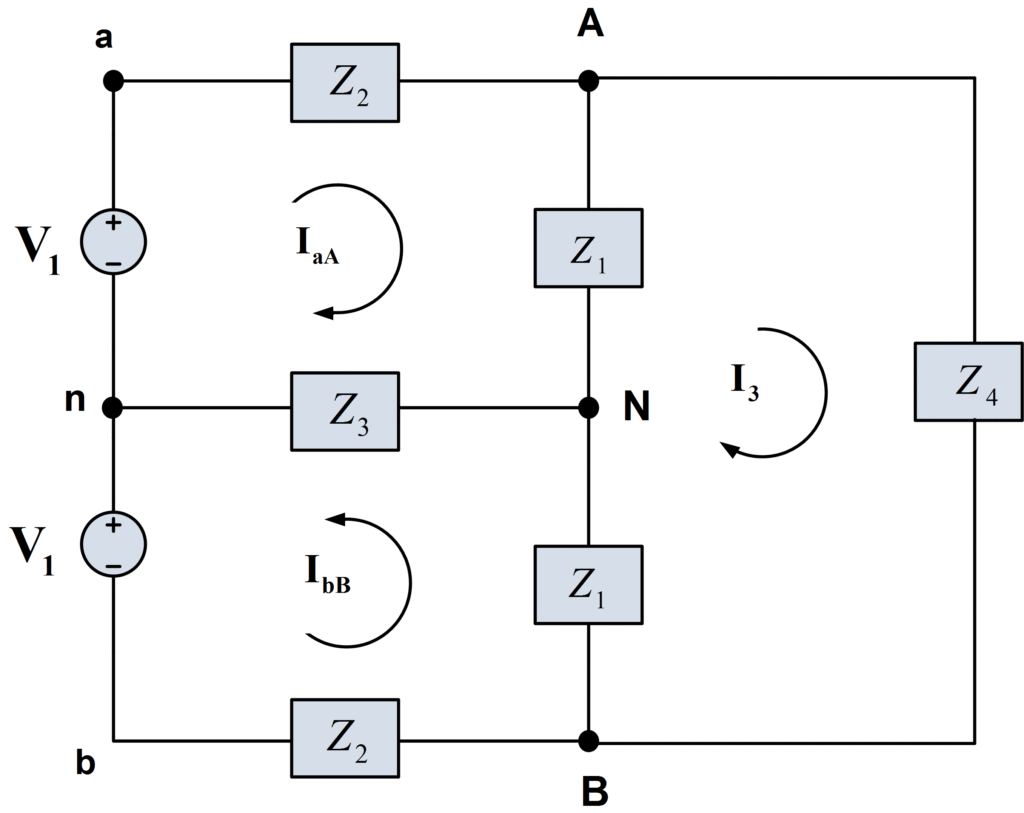
If the lines aA and bB are not perfect conductors but have equal impedances Z2, then InN is still zero because we simply add the series impedances Z1 and Z2 and have essentially the same situation as in figure 4. Indeed, in the more general case shown in figure 5, the neutral current InN is still zero. This may be seen by writing the two mesh equations.
$\begin{align}& ({{Z}_{1}}+{{Z}_{2}}+{{Z}_{3}}){{I}_{aA}}+{{Z}_{3}}{{I}_{bB}}-{{Z}_{1}}{{I}_{3}}={{V}_{1}} \\& {{Z}_{3}}{{I}_{aA}}+({{Z}_{1}}+{{Z}_{2}}+{{Z}_{3}}){{I}_{bB}}+{{Z}_{1}}{{I}_{3}}=-{{V}_{1}} \\\end{align}$
And adding the result, which yield
$({{Z}_{1}}+{{Z}_{2}}+{{Z}_{3}})({{I}_{aA}}+{{I}_{bB}})+{{Z}_{3}}({{I}_{aA}}+{{I}_{bB}})=0$
Or
$\begin{matrix}{{I}_{aA}}+{{I}_{bB}}=0 & \cdots & (5) \\\end{matrix}$
Since by KCL the left member of the last equation is –InN, the neutral current is zero. This is, of course, a consequence of the symmetry of figure 5.
Fig.5: Symmetrical Single-Phase, Three-Wire System
If the symmetry of figure 5 is destroyed by having unequal loads at terminals A-N and N-B or unequal line impedances in lines aA and bB, then there will be a neutral current.
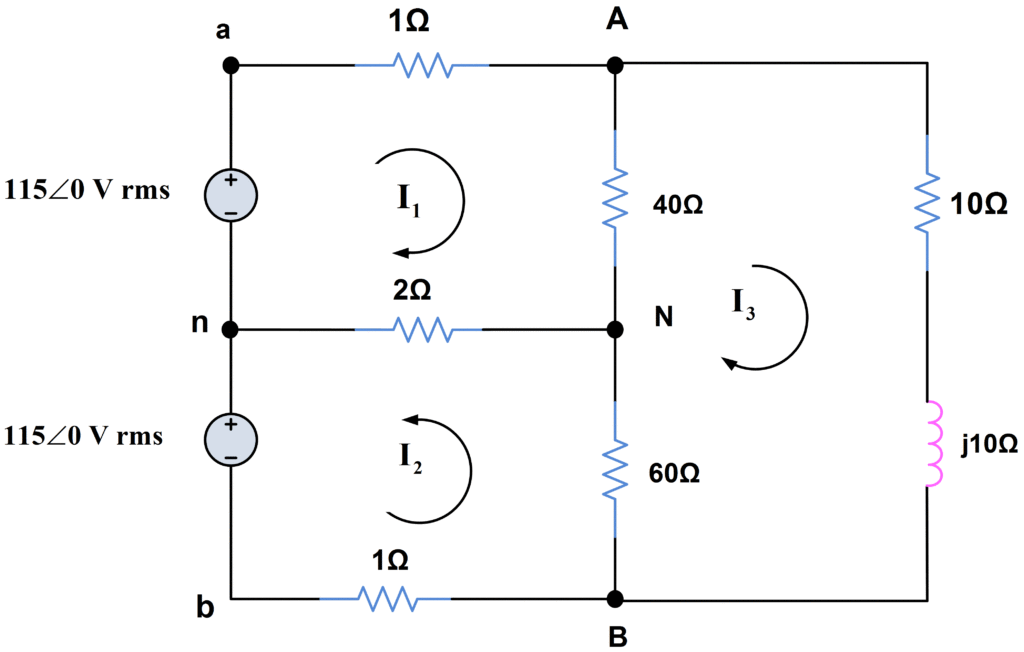
Single Phase, Three Wire System Example
For example, let us consider the situation in figure 6, which has two loads operating at approximately 230 V. the mesh equations are
Fig.6: Single Phase, Three Wire System
$\begin{align}& 43{{I}_{1}}-2{{I}_{2}}-40{{I}_{3}}=115 \\& -2{{I}_{1}}+63{{I}_{2}}-60{{I}_{3}}=115 \\& -40{{I}_{1}}-60{{I}_{2}}+(110+j10){{I}_{3}}=0 \\\end{align}$
Solving for the currents, we have
$\begin{align}& {{I}_{1}}=16.32\angle -{{33.7}^{o}}\text{ A rms} \\& {{I}_{2}}=15.73\angle -{{35.4}^{o}}\text{ A rms} \\& {{I}_{3}}=14.46\angle -{{39.9}^{o}}\text{ A rms} \\\end{align}$
Therefore the neutral current is
${{I}_{nN}}={{I}_{2}}-{{I}_{1}}=0.76\angle {{184.3}^{o}}\text{ }A\text{ }rms$
And, of course, is not zero.