Delta Connection
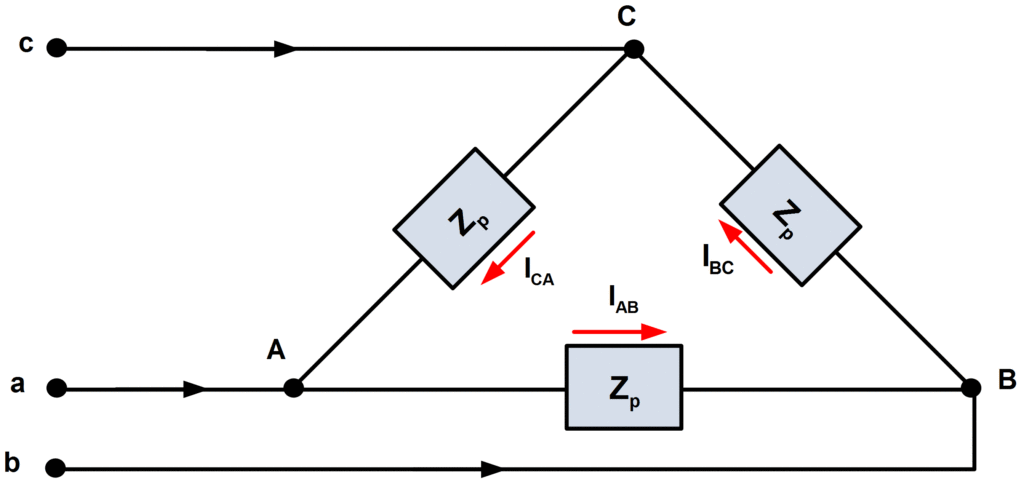
In Delta connection, phase sides are connected in a cyclical arrangement in order to make a closed loop as shown in figure 1. As far as line and phase currents are concerned, they are related to each other as:
${{\text{I}}_{\text{line}}}\text{=}\sqrt{\text{3}}{{\text{I}}_{\text{phase}}}$
Which means that whatever supply current we have, we will have wire cross-section for ${}^{1}/{}_{\sqrt{3}}$ times line current only. Whereas, in Delta connection, line and phase voltage are same:
${{\text{V}}_{\text{phase}}}\text{=}{{\text{V}}_{\text{line}}}$
A balanced delta connected load (with equal phase impedances) is shown in figure 1.
Fig.1: Delta Connected Load
An advantage of a delta connected load over a Y-connected load is that loads may be added or removed readily on a single phase of a delta since the loads are connected directly across the lines. Also, for a given power delivered to the load the phase currents in a delta are smaller than those in a Y. on the other hand, the delta phase voltages are higher than those of the Y connection. Sources are rarely delta connected because if the voltages are not perfectly balanced, there will be a net voltage, and consequently a circulating current, around the delta. This, of course, causes undesirable heating effects in the generating machinery. Also, the phase voltages are lower in the Y-connected generator, and thus less insulation is required. Obviously, systems with delta-connected loads are three wire systems, since there is no neutral connection.
- You May Also Read: Three Phase Star Connection (Y): Three Phase Power,Voltage,Current
Delta Connection Line and Phase Voltages
From figure 1, we see that in the case of delta connected load the line voltages are the same as the phase voltages. Therefore if the line voltages are given by
$\begin{matrix} \begin{align} & {{V}_{ab}}={{V}_{L}}\angle {{30}^{o}} \\ & {{V}_{bc}}={{V}_{L}}\angle -{{90}^{o}} \\ & {{V}_{ca}}={{V}_{L}}\angle -{{210}^{o}} \\\end{align} & \cdots & (1) \\\end{matrix}$
Then the phase voltages are
[stextbox id=”info” caption=”Line and Phase Voltages for Delta Connection”]\[\begin{matrix} \begin{align} & {{V}_{AB}}={{V}_{L}}\angle {{30}^{o}} \\ & {{V}_{BC}}={{V}_{L}}\angle -{{90}^{o}} \\ & {{V}_{CA}}={{V}_{L}}\angle -{{210}^{o}} \\\end{align} & \cdots & (2) \\\end{matrix}\][/stextbox]
Where
$\begin{matrix} {{V}_{L}}={{V}_{p}} & \cdots & (3) \\\end{matrix}$
Delta Connection Line and Phase Currents
If Zp=|Zp|∠θ , then the phase currents are
[stextbox id=”info” caption=”Phase Currents in Delta Connection”]\[\begin{matrix} \begin{align} & {{I}_{AB}}=\frac{{{V}_{AB}}}{{{Z}_{p}}}={{I}_{p}}\angle {{30}^{o}}-\theta \\ & {{I}_{BC}}=\frac{{{V}_{BC}}}{{{Z}_{p}}}={{I}_{p}}\angle -{{90}^{o}}-\theta \\ & {{I}_{CA}}=\frac{{{V}_{CA}}}{{{Z}_{p}}}={{I}_{p}}\angle -{{210}^{o}}-\theta \\\end{align} & \cdots & (4) \\\end{matrix}\][/stextbox]
Where
$\begin{matrix} {{I}_{p}}=\frac{{{V}_{L}}}{\left| {{Z}_{p}} \right|} & \cdots & (5) \\\end{matrix}$
The current in line aA by KCL is
${{I}_{aA}}={{I}_{AB}}-{{I}_{CA}}$
Which after simplifications is
${{I}_{aA}}=\sqrt{3}{{I}_{p}}\angle -\theta $
The other line currents, obtained similarly, are
${{I}_{bB}}=\sqrt{3}{{I}_{p}}\angle -{{120}^{o}}-\theta $
${{I}_{cC}}=\sqrt{3}{{I}_{p}}\angle -{{240}^{o}}-\theta $
Evidently the relation between the line and the phase current magnitudes in the delta case is
$\begin{matrix} {{I}_{L}}=\sqrt{3}{{I}_{p}} & \cdots & (6) \\\end{matrix}$
And the line currents are thus
[stextbox id=”info” caption=”Line Currents in Delta Connection”]\[\begin{matrix} \begin{align} & {{I}_{aA}}={{I}_{L}}\angle -\theta \\ & {{I}_{bB}}={{I}_{L}}\angle -{{120}^{o}}-\theta \\ & {{I}_{cC}}={{I}_{L}}\angle -{{240}^{o}}-\theta \\\end{align} & \cdots & (7) \\\end{matrix}\][/stextbox]
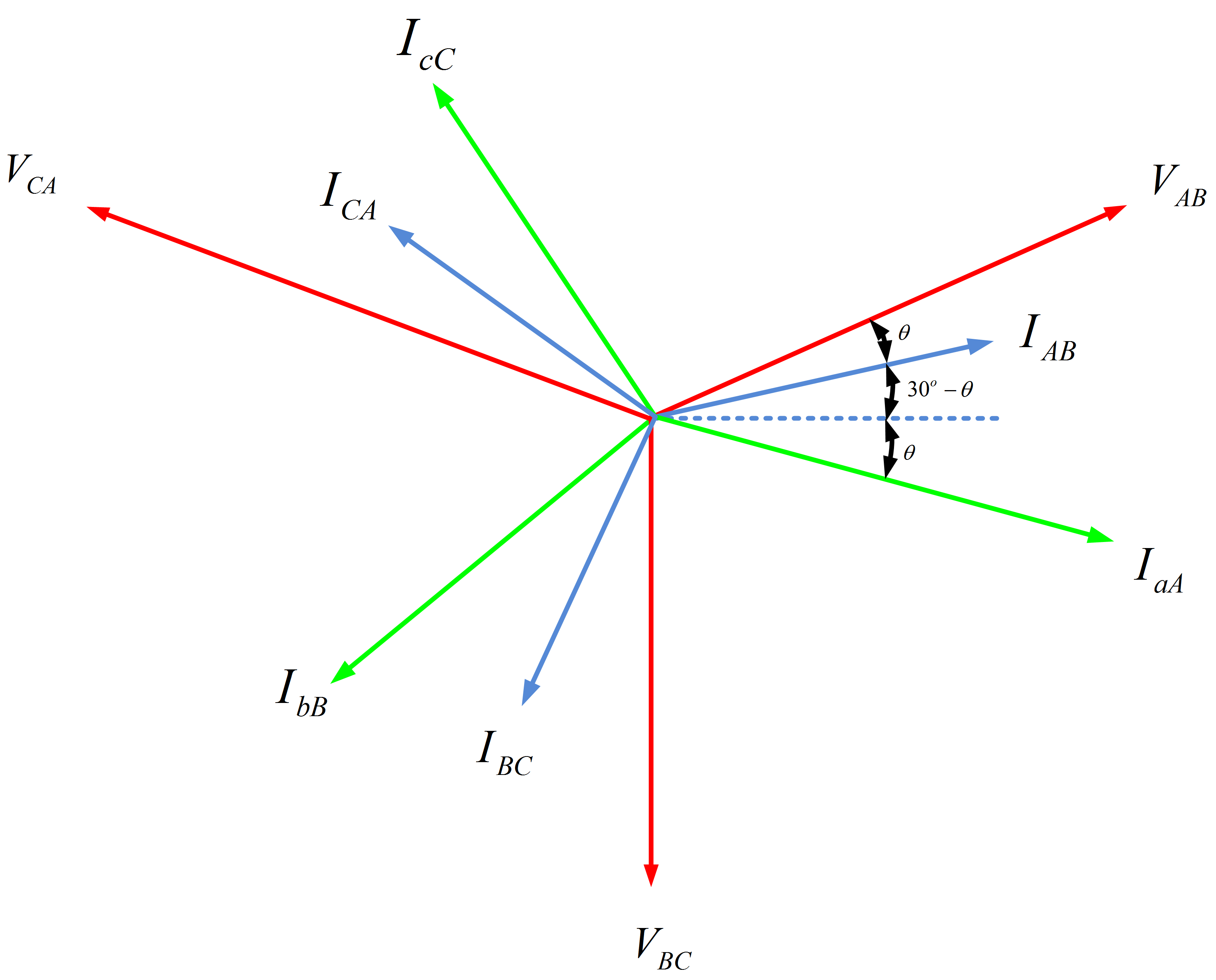
Thus the currents and voltages are balanced sets, as expected. The relationships between line and phase currents for the delta connected load are summed up in the phasor diagram of figure 2.
Fig.2: Phasor Diagram for a Delta-Connected Load
Delta Connection Three Phase Power
Now, let us derive a formula for the power delivered to a balanced three phase load with a power factor angle θ. Whether the load is Y-connected or delta connected, we have
$P=3{{P}_{p}}=3{{V}_{p}}{{I}_{p}}\cos \theta $
In the Y-connected case,
$\begin{align} & {{V}_{p}}={}^{{{V}_{L}}}/{}_{\sqrt{3}} \\ & and \\ & {{I}_{p}}={{I}_{L}} \\\end{align}$
And in the delta connected case,
$\begin{align} & {{I}_{p}}={}^{{{I}_{L}}}/{}_{\sqrt{3}} \\ & and \\ & {{V}_{p}}={{V}_{L}} \\\end{align}$
In either case, then,
$P=3\frac{{{V}_{L}}{{I}_{L}}}{\sqrt{3}}\cos \theta $
Or
[stextbox id=”info” caption=”Three Phase Power”]\[\begin{matrix} P=\sqrt{3}{{V}_{L}}{{I}_{L}}\cos \theta & \cdots & (8) \\\end{matrix}\][/stextbox]
Summary
In Delta-connected case, we have following relations for current and voltages:
$\begin{align} & {{I}_{p}}={}^{{{I}_{L}}}/{}_{\sqrt{3}} \\ & and \\ & {{V}_{p}}={{V}_{L}} \\\end{align}$
In Y-connected case,
$\begin{align} & {{V}_{p}}={}^{{{V}_{L}}}/{}_{\sqrt{3}} \\ & and \\ & {{I}_{p}}={{I}_{L}} \\\end{align}$
Whereas the formula to compute the power in both cases remains the same which is
$P=\sqrt{3}{{V}_{L}}{{I}_{L}}\cos \theta $