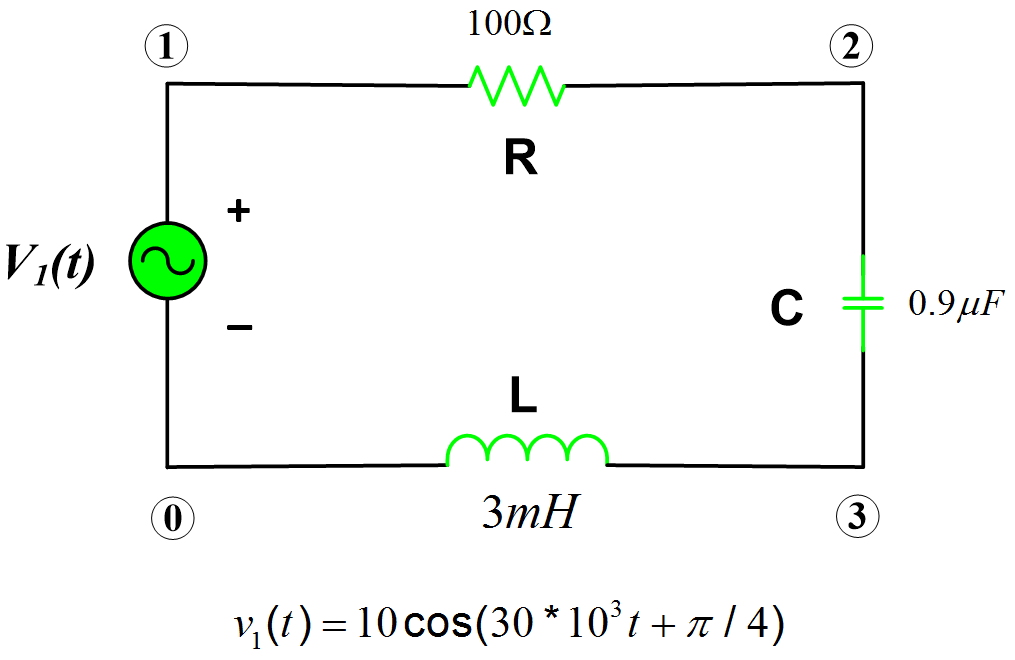
In this tutorial, we will determine the voltages at each node of the following circuit using Matlab.
Determine the voltage at each node of the circuit of figure:
The impedances correspond to an inductor and capacitor in the above circuit can be obtained using the following expressions:
$\begin{align} & {{Z}_{C}}={{\left. \frac{1}{j\omega C} \right|}_{\omega =30\text{ krad/s}}} \\ & {{Z}_{L}}={{\left. j\omega L \right|}_{\omega =30\text{ krad/s}}} \\\end{align}$
From the voltage expression, we can obtain the phasor value as:
$V=10\exp (j\frac{\pi }{4})\text{ V}$
For the current, we have the following expression:
$I=\frac{V}{R+{{Z}_{C}}+{{Z}_{L}}}$
Now, the voltage across each element in the circuit can be obtained as:
$\begin{align} & {{V}_{R}}=IR \\ & {{V}_{C}}=Z{}_{C}I \\ & {{V}_{L}}={{Z}_{L}}I \\\end{align}$
Now, let’s formulate above mentioned equations in Matlab:
Matlab Code for Voltage Calculation in an AC Circuit
%Simple AC Circuit clear all;close all;clc Voltage= 10*exp(j*pi/4); % Source Voltage Omega=30e3; % Angular Frequency R= 100; % Circuit Resistance L= 3e-3; % Circuit Impedance (3mH) C= 0.9e-6; % Circuit Capacitance (0.9 microFarad) Zc= 1/(j*Omega*C); % Capacitive Reactance Zl= j*Omega*L; % Inductive Reactance I= Voltage/(Zl+Zc+R) % Total Circuit Current VR= I*R % Voltage across Resistor VL= I*Zl % Voltage across an Inductor VC= I*Zc % Voltage across Capacitor %=============================================
Results:
VR =
8.4467 + 2.5974i
VL =
-2.3377 + 7.6021i
VC =
0.9620 – 3.1284i
You May Also Read: RLC Circuit Transfer Function using Matlab