This article introduces the concept of decibels and their application in measuring amplifier gain, explaining the use of logarithmic scaling in sound systems and electronics.
Logarithmic Gain
The human ear does not respond to sound levels in the same manner as an amplifying system. An amplifier, for example, has a linear rise in signal level. An input signal level of 1 V can produce, for example, an output of 10 V. The voltage amplification then is 10:1, or 10. The human ear, however, does not respond in a linear manner. It is, essentially, a nonlinear device. As a result of this, sound amplifying systems are usually evaluated on a logarithmic scale. This type of scale illustrates how our ears actually respond to specific signal levels. Gain expressed in logarithms, therefore, is much more meaningful than linear gain relationships.
The logarithm of a given number is the power to which another number, called the base, must be raised to equal the given number. Basically, a logarithm has the same meaning as an exponent. A common logarithm is expressed in powers of 10. This is illustrated by the following:
$$10^{3} = 1000$$
$$10^{2} = 100$$
$$10^{1} = 10$$
$$10^{0} = 1$$
This means that the logarithm of any number between 1000 and 9999 has a characteristic value of 3. The characteristic is an expression of the magnitude range of the number. Numbers between 100 and 999 have a characteristic of 2. Numbers between 10 and 99 have a characteristic of 1. Between 1.0 and 9.0, the characteristic is 0. Numbers less than 1.0 have a negative characteristic. It is generally not customary in electronics to use negative characteristic values.
When a number is not an even multiple of 10, its log is a decimal. The decimal part of the logarithm is called the mantissa. The log of a number such as 4000 is expressed as 3.6021. The characteristic is 3 because 4000 is between 1000 and 9999. The mantissa of 4000 is 0.6021. To find this value, simply use the [log] key and the proper key sequence on a scientific calculator. The log of 4000 is 3.6021, expressed as $\log_{10} 4000 = 3.6021$, or simply as $\log 4000 = 3.6021$. The characteristic is 3, and the mantissa is 0.6021.
The mantissa is always the same for numbers that are identical, except for the location of the decimal point. For example, the mantissa is the same for 1630, 163.0, 16.3, 1.63. The only difference in these values is the characteristic. The mantissa for 1.63 is 0.2122, and the characteristic is 0. The log is, therefore, 0.2122. The logs of the five values given are 3.2122, 2.2122, 1.2122, and 0.2122, respectively.
Understanding Decibels in Amplification
Consider now the gain of a sound system with several stages of amplification. Gain is best expressed as a ratio of two signal levels. Specifically, gain is expressed as the output level divided by the input level. This is determined by the following expression:
$$A_{P} = \log_{10} \left( \frac{P_{\text{out}}}{P_{\text{in}}} \right) \text{ (in Bels)}$$
For an amplifier with 0.1 W of input and 100 W of output:
$$A_{P} = \log_{10} \left( \frac{100}{0.1} \right) = \log_{10} 1000 = 3\ \text{B}$$
As you can see, the Bel represents a rather large ratio in sound level. A decibel (dB) is a more practical measure of sound level. A decibel is one-tenth of a Bel. The Bel is named for Alexander Graham Bell, the inventor of the telephone.
The gain of a single stage of amplification within a system can be determined in decibels. A single amplifier stage might have an input of 10 mW and an output of 150 mW. The power gain in decibels is determined by the following formula:
$$A_{P} = 10 \log_{10} \left( \frac{P_{\text{out}}}{P_{\text{in}}} \right) \text{ dB}$$
$$A_{P} = 10 \log_{10} \left( \frac{150}{10} \right) = 10 \log_{10} 15 = 10 \times 1.1761 = 11.761\ \text{dB}$$
If the input power applied to an amplifier and the power gain are known, the output power can be calculated. Consider, for example, an amplifier with $P_{\text{in}} = 10\ \text{mW} \quad$ and $\quad A_{P} = 11.761\ \text{dB}$.
$$ A_{P}= 10 \log_{10} \left( \frac{P_{\text{out}}}{P_{\text{in}}} \right) \text{ dB}$$
$$\frac{A_{P}}{10} = \log_{10} \left( \frac{P_{\text{out}}}{P_{\text{in}}} \right) $$
$$10^{\frac{A_{P}}{10}} = \frac{P_{\text{out}}}{P_{\text{in}}} $$
$$P_{in} \times 10^{\frac{A_{P}}{10}} = \frac{P_{\text{out}}}{P_{\text{in}}} $$
$$P_{\text{out}} = P_{\text{in}} \times 10^{0.1 \times A_{P}}$$
$$P_{\text{out}} = 10\ \text{mW} \times 10^{0.1 \times 11.761} = 10\ \text{mW} \times 15.0 = 150\ \text{mW}$$
Voltage Gain in Decibels
The voltage gain of an amplifier can also be expressed in decibels. To do this, the power-level expression must be adapted to accommodate voltage values. The voltage gain formula is:
$$A_{V} = 20 \log_{10} \left( \frac{V_{\text{out}}}{V_{\text{in}}} \right) \text{ dB}$$
Power is expressed as $V^2/R$. Power gain using voltage and resistance values is, therefore, expressed as:
$$A_{P} = 10 \log_{10} \left( \frac{V^2_{\text{out}}/R_{\text{out}}}{V^2_{\text{in}}/R_{\text{in}}} \right)$$
If the values of $R_{\text{in}} \quad$ and $\quad R_{\text{out}}$ are equal, the voltage gain expression simplifies to:
$$A_{V} = 2 \times 10 \log_{10} \left( \frac{V_{\text{out}}}{V_{\text{in}}} \right) = 20 \log_{10} \left( \frac{V_{\text{out}}}{V_{\text{in}}} \right) \text{ dB}$$
If the input voltage applied to an amplifier and the voltage gain are known, the output voltage can be calculated.
Consider an amplifier with $V_{\text{in}} = 5\ \text{mV} \quad$ and $ \quad A_{V} = 15\ \text{dB}$:
$$V_{\text{out}} = V_{\text{in}} \times 10^{0.05 \times A_{V}} = 5\ \text{mV} \times 10^{0.75} = 5\ \text{mV} \times 5.623 = 28.11\ \text{mV}$$
It is important to remember that decibel voltage gain assumes the values of $R_{\text{in}}$ and $R_{\text{out}}$ to be equal. Decibel gain is primarily an expression of power levels. Voltage gain is, therefore, only an adaptation of the power-level expression.
Example 2
What is the decibel voltage gain of the first amplifier in Figure 1?
Solution
The input voltage is 0.25 Vpp, and the output voltage is 1.25 Vpp:
$$A_{V} = 20 \log_{10} \left( \frac{1.25}{0.25} \right) = 20 \log_{10} 5 = 20 \times 0.6989 = 13.979$$
Example 3
What is the total decibel voltage gain of the three amplifiers in Figure 1?
Solution
Determine the decibel voltage gain of the third amplifier. The input voltage is 6.25 Vpp and the output voltage is 25 Vpp:
$$A_{V} = 20 \log_{10} \left( \frac{25}{6.25} \right) = 20 \log_{10} 4 = 20 \times 0.6021 = 12.041\ \text{dB}$$
Determine the total decibel voltage gain by adding the decibel gain of all three amplifiers:
$$A_{V(\text{total})} = 13.979 + 13.979 + 12.041 = 40\ \text{dB}$$
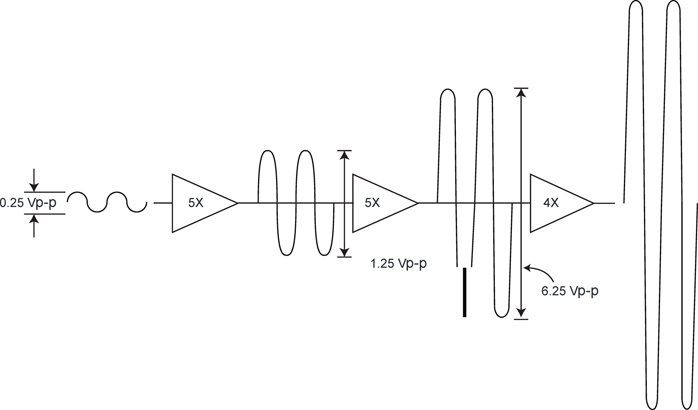
Figure 1. Three-Stage Voltage Amplifier
Review Questions
- The logarithm of a number such as 4000 is expressed as ______.
- A decibel is equal to ______ of a Bel.
- Power gain in decibels is given by the formula ______.
- The mantissa of 1.63 is ______.
- Voltage gain in decibels is expressed as ______.
- If $V_{\text{in}} = 5\ \text{mV}$ and $A_{V} = 15\ \text{dB}$, then $V_{\text{out}}$ is ______.
- The total gain of three amplifier stages is found by ______.
Answers
- 3.6021
- one-tenth
- $10 \log_{10} (P_{\text{out}} / P_{\text{in}})$
- 0.2122
- $20 \log_{10} (V_{\text{out}} / V_{\text{in}})$
- 28.11 mV
- adding individual stage gains
Key Takeaways
Understanding decibel gain and logarithmic scaling is vital in electronics and sound engineering, as it aligns technical measurements with human hearing perception. These concepts simplify calculations and system evaluations, especially when dealing with amplification, power levels, and voltage variations in multi-stage electronic systems.