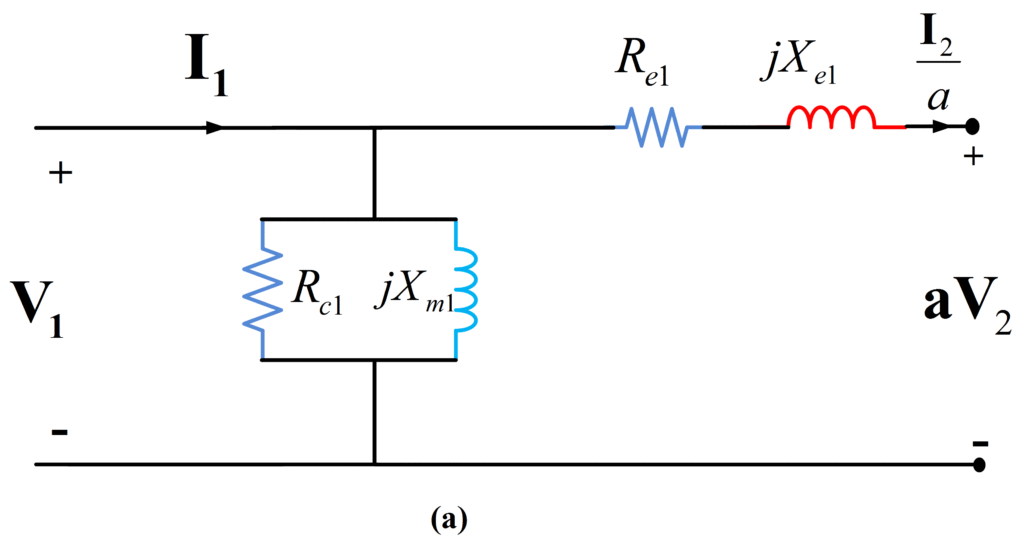
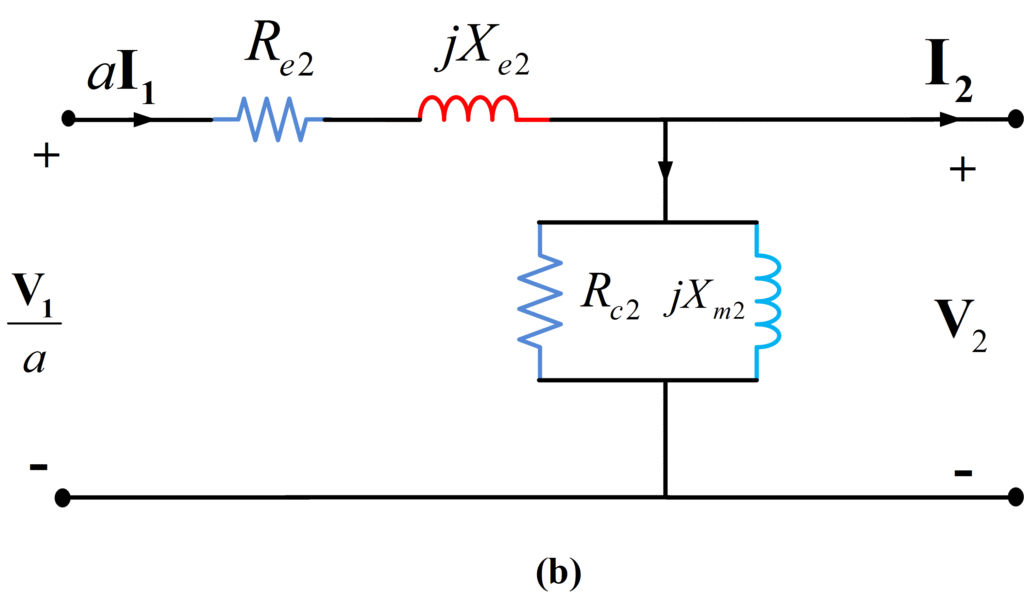
In order for a model to be useful, there must be a way to determine the values of the model parameters. Two simple tests are used to determine the values for the parameters of the transformer equivalent circuit of Fig. 1 (a) and (b). The two tests are the short-circuit and open-circuit tests.
Fig.1: Approximate Equivalent Circuit (a) and (b)
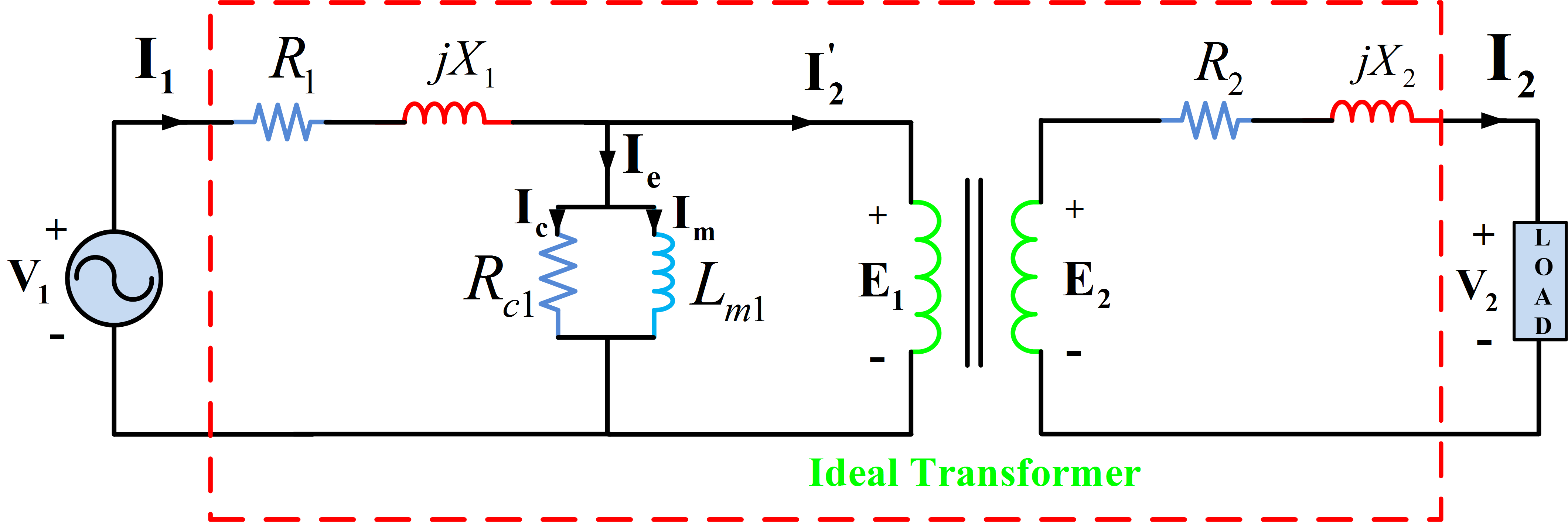
If it is desired to find the parameters of the exact equivalent circuit of Fig. 2, it is customary to assume R1=a2R2 and X1 =a2X2. This assumption allows the decomposition of the equivalent resistance and reactance into the primary and secondary components.
Fig.2: Transformer Equivalent Circuit in Phasor Form
Let the primary (winding 1) be the high-voltage side and the secondary (winding 2) the low-voltage side for the transformer of Fig.3.
Fig.3: An Actual Transformer
- You May Also Read: Equivalent Circuit of Transformer Referred to Primary and Secondary Side
Transformer Open-Circuit Test
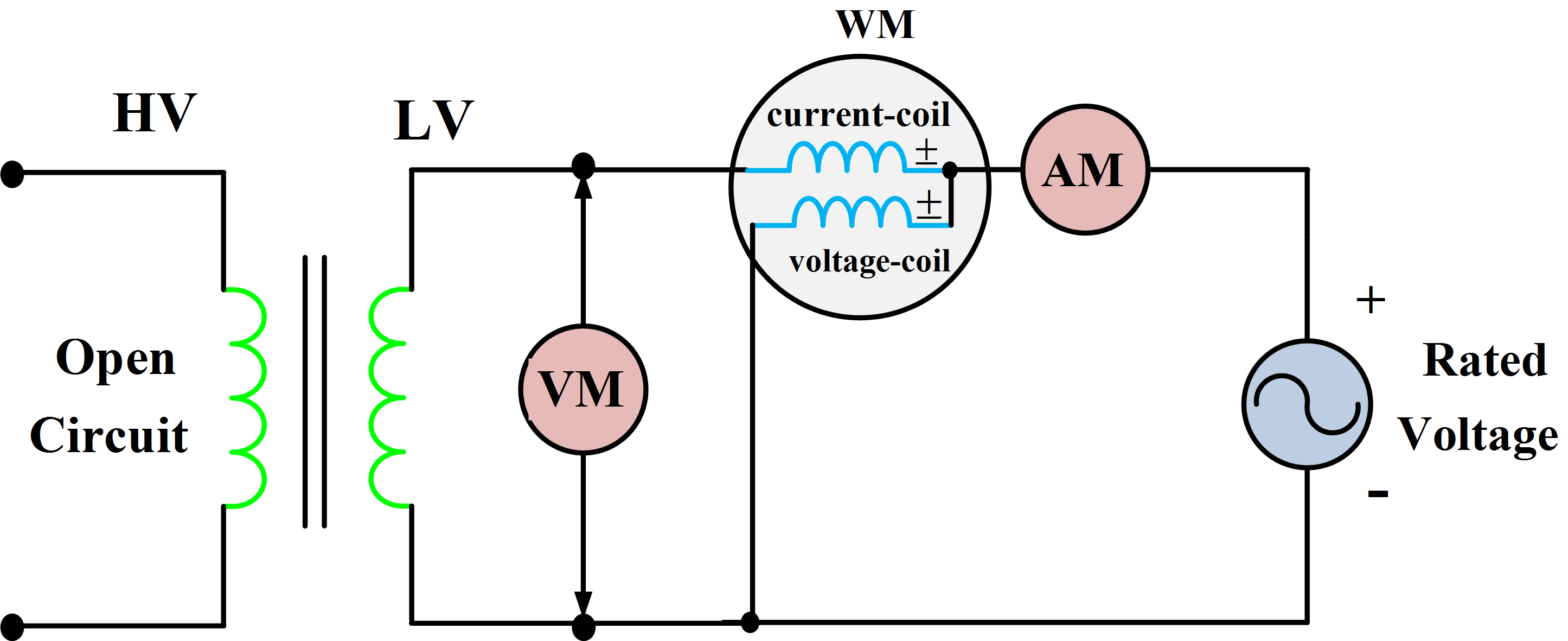
In the open-circuit test, the transformer rated voltage is applied to the low-voltage side of the transformer with the high-voltage side left open. Measurement of power, current, and voltage are made on the low-voltage side as shown in Fig.4.
Fig.4: Connections for Open Circuit Test
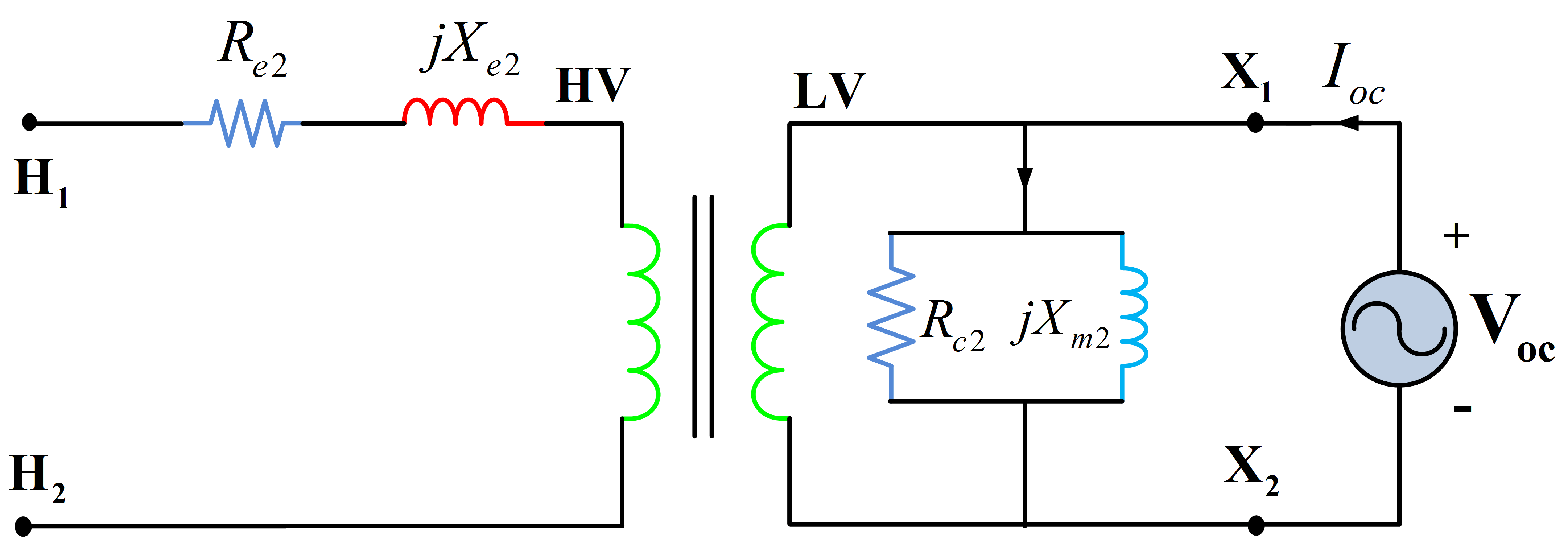
Since the high-voltage side is open, the input current Ioc is equal to the exciting current through the shunt excitation branch as shown in the equivalent circuit of Fig 5. Because this current is very small, about 5% of rated value, the voltage drop across the low-voltage winding and the winding copper losses are neglected.
Fig.5: Equivalent Circuit for Open Circuit Test
The magnitude of the admittance of the shunt excitation branch of the equivalent circuit referred to the low-voltage side is calculated as follows:
\[\begin{matrix} \left| {{Y}_{o2}} \right|=\frac{{{I}_{oc}}}{{{V}_{oc}}} & {} & \left( 1 \right) \\\end{matrix}\]
The phase angle of the admittance is found as
\[\begin{matrix} -{{\theta }_{o2}}=-{{\cos }^{-1}}\left( \frac{{{P}_{oc}}}{{{V}_{oc}}{{I}_{oc}}} \right) & {} & \left( 2 \right) \\\end{matrix}\]
Thus, the complex admittance may be expressed as
$\begin{matrix} {{Y}_{o2}}=\left| {{Y}_{o2}} \right|\angle -{{\theta }_{o2}}={{G}_{c2}}-j{{B}_{m2}} & {} & \left( 3 \right) \\\end{matrix}$
The corresponding resistance and reactance parameter of Fig. 1 (b) are derived from the conductance and susceptance, respectively:
\[\begin{matrix} {{R}_{c2}}=\frac{1}{{{G}_{c2}}} & {} & \left( 4 \right) \\\end{matrix}\]
\[\begin{matrix} j{{X}_{m2}}=\frac{1}{-j{{B}_{m2}}} & {} & \left( 5 \right) \\\end{matrix}\]
These parameters may be referred to the high-voltage side to give the parameters of the equivalent circuit of Fig. 1 (a).
$\begin{matrix} {{R}_{c1}}={{a}^{2}}{{R}_{c2}} & {} & \left( 6 \right) \\\end{matrix}$
$\begin{matrix} {{X}_{m1}}={{a}^{2}}{{X}_{m2}} & {} & \left( 7 \right) \\\end{matrix}$
Note that when a rated voltage at the rated frequency is applied during the open-circuit test, the power input Poc is practically equal to the rated core loss. It most applications, this value of core loss is typically assumed to remain constant for different load levels.
Transformer Short-Circuit Test
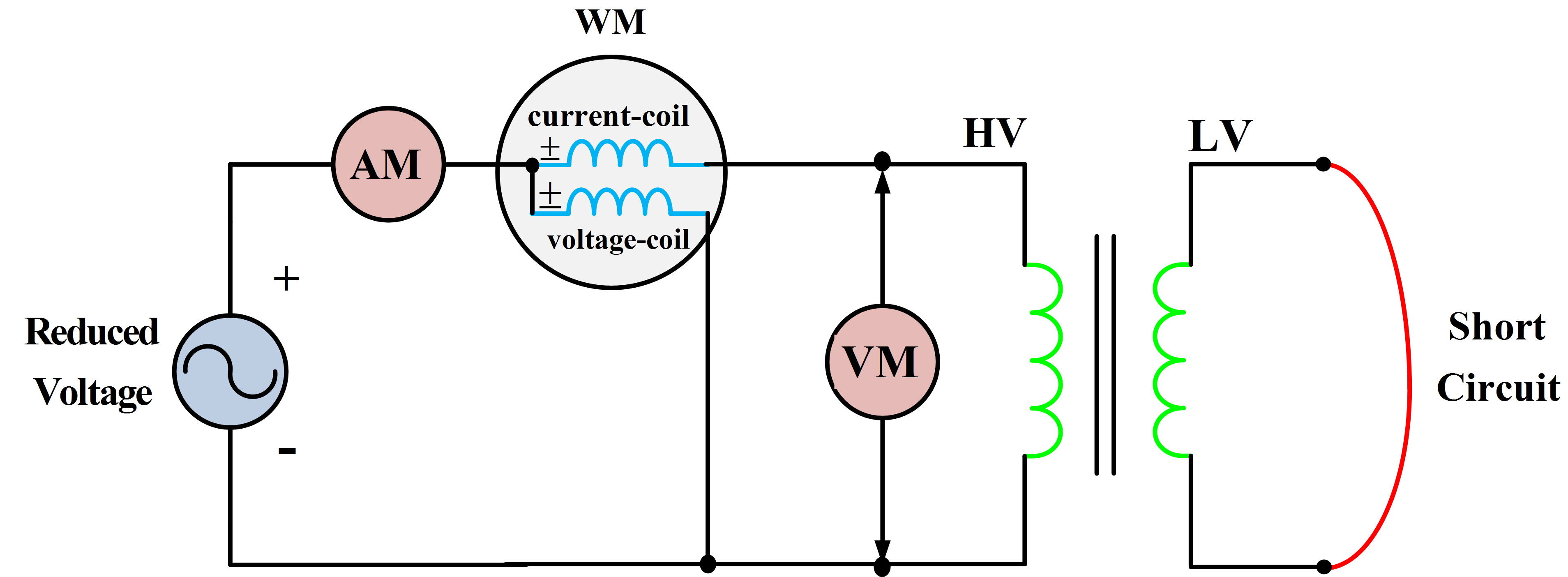
In the short-circuit test, the low-voltage side is short-circuited and the high-voltage side is connected to a variable, low-voltage source. Measurements of power, current, and voltage are made on the high-voltage side as shown in Fig. 6.
Fig.6: Connections for Short Circuit Test
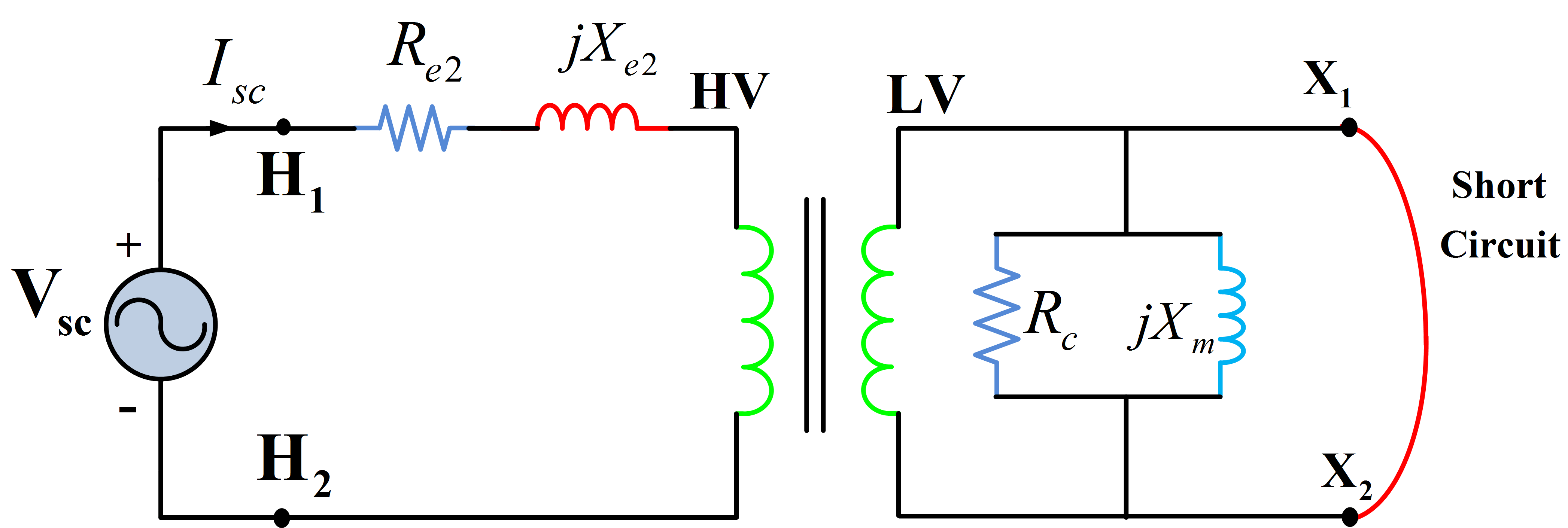
The applied voltage is adjusted until rated short-circuit current flows in the windings. This voltage is generally much smaller than the rated voltage, in the range of 0.05 to 0.10 per unit. Therefore, the current through the magnetizing branch is negligible, and the applied voltage may be assumed to occur wholly as a voltage drop across the transformer series impedance as shown in the equivalent circuit of Fig.7.
Fig.7: Equivalent Circuit for Short Circuit Test
The magnitude of the series impedance of referred to the high-voltage (primary) side may be calculated as follows:
\[\begin{matrix} \left| {{Z}_{e1}} \right|=\frac{{{V}_{sc}}}{{{I}_{sc}}} & {} & \left( 8 \right) \\\end{matrix}\]
The equivalent series resistance referred to the high-voltage side is
\[\begin{matrix} {{R}_{e1}}=\frac{{{P}_{sc}}}{I_{sc}^{2}}={{R}_{1}}+{{a}^{2}}{{R}_{2}} & {} & \left( 9 \right) \\\end{matrix}\]
Corresponding equivalent series reactance referred to the high-voltage side is
\[\begin{matrix} {{X}_{e1}}=\sqrt{{{\left| {{Z}_{e1}} \right|}^{2}}-R_{e1}^{2}}={{X}_{1}}+{{a}^{2}}{{X}_{2}} & {} & \left( 10 \right) \\\end{matrix}\]
The values of these parameters derived from the short-circuit test are used in conjunction with Fig. 1(a). These parameters may be referred to the low-voltage (secondary) side to derive the corresponding values for use with Fig. 1 (b) as follows:
\[\begin{matrix} {{R}_{e2}}=\left( \frac{1}{{{a}^{2}}} \right){{R}_{e1}} & {} & \left( 11 \right) \\\end{matrix}\]
\[\begin{matrix} {{X}_{e2}}=\left( \frac{1}{{{a}^{2}}} \right){{X}_{e1}} & {} & \left( 12 \right) \\\end{matrix}\]
Note that when rated current flows through the windings during the short-circuit test, the power input Psc is equal to the rated copper loss.
Tests on Three-phase Transformers
When a three-phase transformer under-goes open-circuit and short-circuit tests, it must be remembered that the power being measured is total three-phase power, the measured voltage is line-to-line voltage, and the measured current is line current. The impedance parameters of interest are to be calculated on a per-phase basis. Therefore, before using the formulas derived above to calculate the resistances and reactances, the measured values must also be converted to per-phase values.
- You May Also Read: Transformer Working Principle | How Transformer Works