The article explores the concept of voltage regulation in transformers, defining it as the change in output voltage from no-load to full-load conditions. It discusses the factors influencing voltage regulation, such as load characteristics and power factor, and provides mathematical formulations to quantify voltage regulation. Additionally, it highlights the implications of leading power factor loads, where voltage regulation can become negative, posing challenges to system stability and efficiency.
What is the Voltage Regulation of a Transformer?
The voltage regulation of a transformer can be described as the change in the secondary voltage as the current varies from full load to no load while keeping the primary voltage constant.
Generally, a transformer is utilized to supply loads that operate at basically constant voltage. The amount of secondary (load) current which is drawn entirely depends on the load linked to the transformer secondary side terminals. As this current varies with changing load, with the same applied primary voltage, the load voltage varies accordingly. This change in the load voltage is primarily due to the voltage drop across the transformer internal impedance. Voltage regulation is actually a measure of how much the voltage varies as the load is varied.
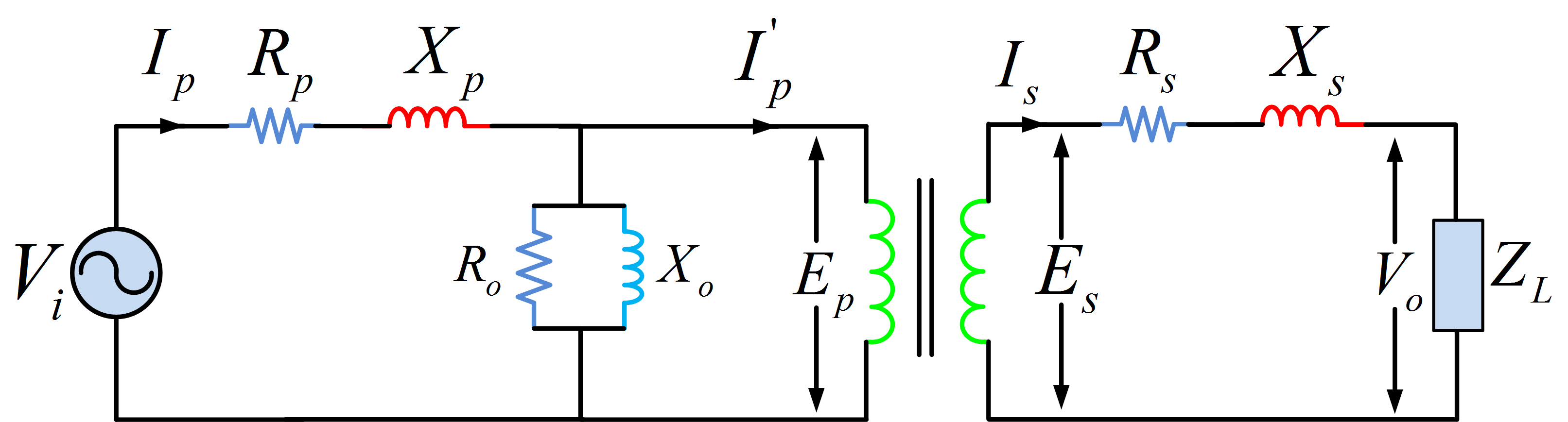
It is clear from the transformer equivalent circuit in Figure 1 that the secondary current Is produces voltage drop IsRs and Is Xs across the resistive and reactive components respectively. Also, the primary current Ip causes primary circuit voltage drops IpRp and IpXp. Consequently, the effective primary voltage Ep is less than the input voltage Vi, and the output voltage Vo is less than the calculated value of Es.
Figure 1: Complete Equivalent Circuit Diagram of Transformer
It appears that the transformer output voltage is greatest on no-load and that under loaded conditions the voltage drop across resistive and reactive components of the equivalent circuit cause Vo to drop below its no-load level. (Note that, depending on the power factor of the load, the output full-load voltage may actually be larger than the no-load voltage).
Voltage Regulation of Transformer Formula
The percentage change in output voltage from no-load to full-load is termed the voltage regulation of the transformer. Ideally, there should be no change in Vo from no-load to full-load (i.e., regulation = 100%). For the best possible performance, the transformer should have the lowest possible regulation. Mathematically, voltage regulation can be expressed as
\[\begin{matrix} Voltage\text{ }Regulation=\frac{{{V}_{o(NL)}}-{{V}_{o(FL)}}}{{{V}_{o(FL)}}} & {} & \left( 1 \right) \\\end{matrix}\]
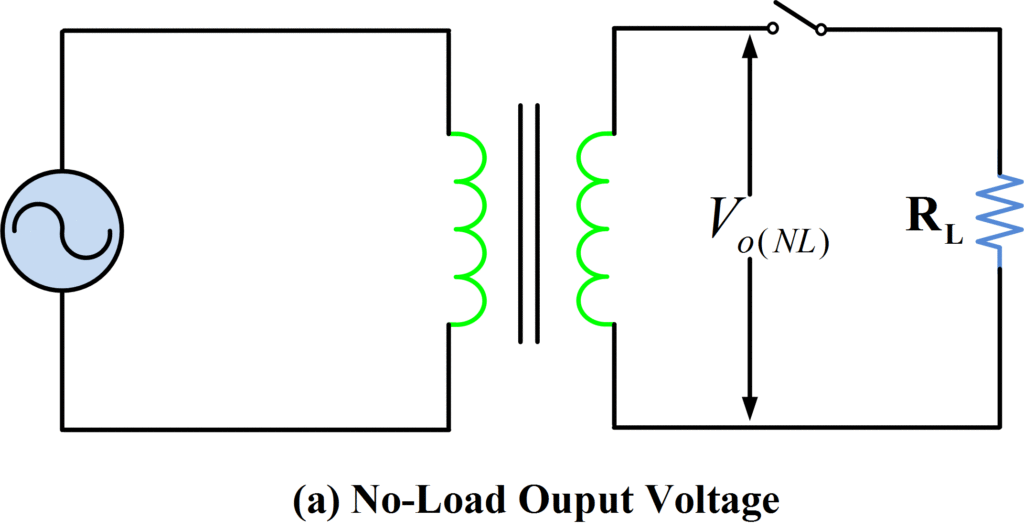
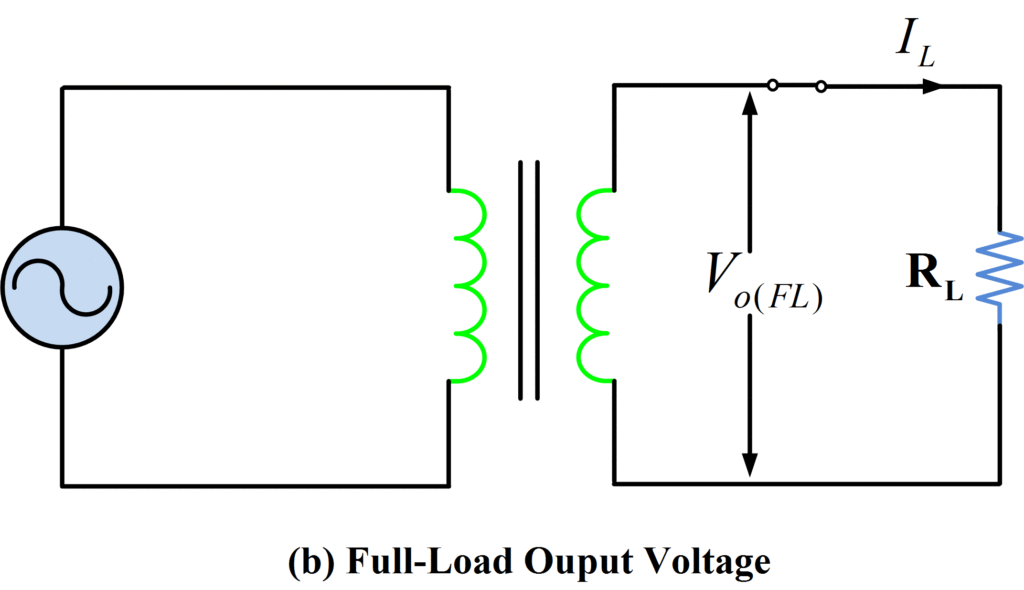
Where Vo(NL) is the transformer no-load output voltage, and Vo(FL) is the full load output voltage. Voltage regulation for a transformer is illustrated in figure 2.
Figure 2: Transformer No-Load and Full-Load Output Voltage
- You May Also Read: Transformer Losses and Efficiency Calculation
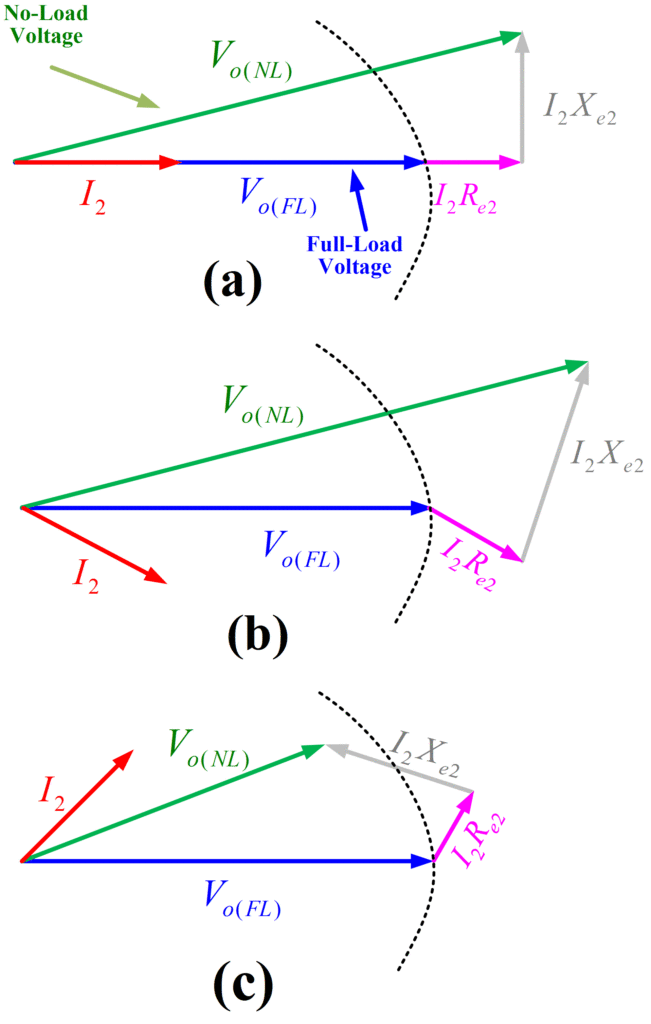
The three phasor diagrams of Figure 3 illustrate how the voltage regulation depends on the power factor of the load. In diagram (a), the current is in phase with the voltage (the load is resistive and its power factor is unity), whereas in diagram (b), the current lags the voltage (the load is inductive, the power factor is called lagging), and in diagram (c), the current leads the voltage (the load is capacitive, the power factor is said to be leading).
Figure 3: Voltage Regulation of Transformer at (a) Unity (b) Lagging (c) Leading Power Factor
Voltage Regulation of Transformer at Unity Power Factor
Figure 3 (a) shows a phasor diagram for the case of a resistive load (unity power factor) on the transformer (i.e., the load current is in phase with the secondary voltage). Since the current I2 is in phase with the secondary voltage Vo (FL), the voltage drop across Re2 is also in phase with Vo (FL). The drop across the leakage reactance Xe2 leads the secondary voltage Vo (FL) by 90o, as shown. The circular arc has a radius equal to Vo (FL) and therefore represents a line of constant secondary voltage. The referred value of primary voltage Vo (NL) is beyond the arc, so it is bigger than the secondary voltage Vo (FL), which means the voltage regulation calculated by equation (1) is positive.
Voltage Regulation of Transformer at Lagging Power Factor
Figure 3 (b) shows a phasor diagram for the case of an inductive load (lagging power factor) on the transformer (i.e., the load current lags the secondary voltage by 90o). The referred value of primary voltage Vo (NL) is beyond the arc, so it is bigger than the secondary voltage Vo (FL), which means the voltage regulation calculated by equation (1) is positive for an inductive case. For any current that lags the secondary voltage by 0 to 90o, the voltage regulation will be positive.
Voltage Regulation of Transformer at Leading Power Factor
Figure 3 (c) shows a phasor diagram for the case of a capacitive load (leading power factor) on the transformer i.e., the load current leads the secondary voltage by 90o. As a result, the referred value of primary voltage Vo (NL) is actually smaller than the secondary voltage Vo (FL), which means the voltage regulation calculated by equation (1) is negative for a capacitive case.
Negative Voltage Regulation in Transformers
Negative voltage regulation can only occur with leading power factor loads; however, not all leading loads will cause negative voltage regulation.
Negative voltage regulation means the voltage increases with the load.
This is a very undesirable condition because it can lead to an unstable condition. Many loads use more power as the voltage increases. Thus, the voltage goes up, causing the power to go up, potentially causing the voltage to go up some more.
Many utilities impose a penalty on large customers if they operate at a leading power factor. Most loads are lagging, so leading power factor usually results from a failure to remove power factor correction capacitors when the load decreases.
- You May Also Read: Transformer Polarity Test