Nodal analysis or Node voltage method uses node voltages as circuit variables in order to analyze the circuit.
The objective of this section is to obtain a set of simultaneous linear equations. However, unlike the mesh analysis method, the procedure developed in this section depends on the choice of certain voltages used as variables in conjunction with Kirchhoff’s current law (KCL). This method of solving problem is called nodal analysis.
A general procedure for analyzing a network by nodal analysis is as follows;
- Convert all voltage sources to current sources.
- Indicate one node as a reference node. This reference node is used as the common point in the network from which the node voltages are measured as shown in fig.
The number of node voltages and thus the number of linear equations is given by
N-1
Where N is the total number of nodes in the network.
- At each node, except the reference node, apply the Kirchhoff’s current law (KCL)
- Solve the set of simultaneous linear equations for the node voltages.
- You May Also Read: Mesh-Current Method
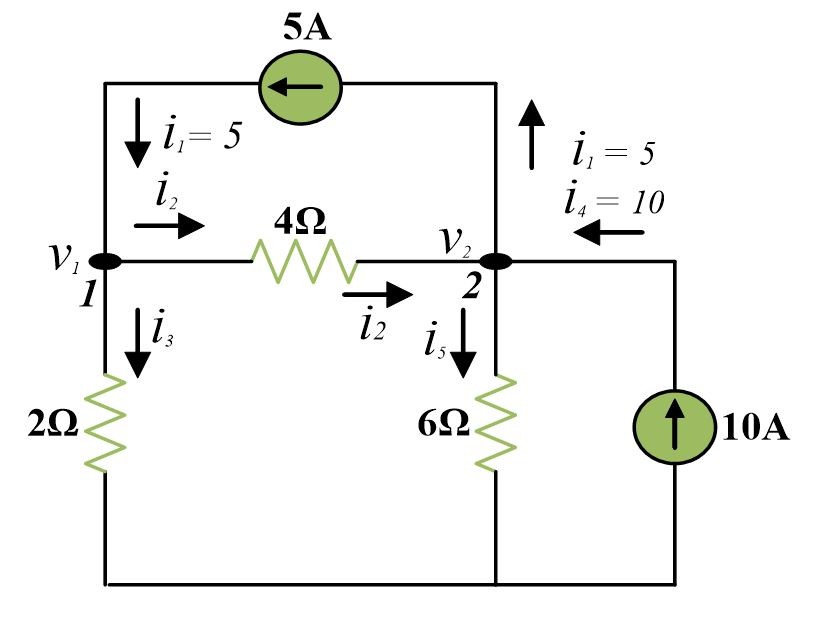
Example of Nodal Analysis
Calculate node voltages V1 and V2
At Node 1, Apply KCL
${{i}_{1}}={{i}_{2}}+{{i}_{3}}$
Using Ohms’ Law,
$\frac{{{V}_{1}}-{{V}_{2}}}{4}+\frac{{{V}_{1}}-0}{2}=5$
$3{{V}_{1}}-{{V}_{2}}=20~~~\text{ }\cdots ~~~\left( 1 \right)$
At Node 2, Apply KCL
${{i}_{1}}+{{i}_{5}}={{i}_{2}}+{{i}_{4}}$
Using ohm’s law,
$\frac{{{V}_{2}}-0}{6}+5=\frac{{{V}_{1}}-{{V}_{2}}}{4}+10$
$-3{{V}_{1}}+5{{V}_{2}}=60~~~\text{ }\cdots \text{ }~~\left( 2 \right)$
Solving (1) and (2), we have
${{V}_{1}}=13.33~V$
${{V}_{2}}=20~V$
And currents are
${{i}_{1}}=5A$
${{i}_{2}}=\frac{{{V}_{1}}-{{V}_{2}}}{4}=-1.6668~A$
${{i}_{3}}=\frac{{{V}_{1}}}{2}=6.666~A$
${{i}_{4}}=10~A$
${{i}_{5}}=\frac{{{V}_{2}}}{6}=3.333~A$
It is sometimes convenient to choose the node at the bottom of a network or the node which has the largest number of branches connected to it. The node having the largest number of branches connected to it produces a node equation with the largest number of terms so that choosing it as a reference eliminates it from further consideration.
- You May Also Read: Nodal Analysis using Matlab