The method of symmetrical components is employed to analyze power systems with unbalanced polyphase voltages and currents. It involves resolving the unbalanced set of phasors into three balanced sets: positive sequence, negative sequence, and zero sequence. The positive and negative sequences consist of three phasors with equal magnitudes separated by 120 degrees, while the zero sequence comprises three in-phase phasors. By representing the unbalanced phasors using sequence components, a matrix formulation is derived to simplify the analysis of power systems in the presence of asymmetry.
The method of symmetrical components is used to solve power system problems involving unbalanced polyphase voltages and currents. It is analogous to the Fourier analysis of nonsinusoidal wave shapes wherein a non-sine wave is resolved into a number of sine waves of various frequencies.
In symmetrical components, the unbalanced set of polyphase phasors is resolved into a number of balanced sets of phasors. After the unbalanced sets of voltage and current phasors are resolved into their symmetrical components, the power system may be solved using per-phase analysis.
A balanced, or symmetrical, set of phasors is defined as a set of phasors that have equal magnitudes and are separated by equal angles. Thus, the phasors in a three-phase balanced set are separated from each other by an angle of 120°.
In a three-phase system, an unbalanced set of phasors is resolved by using three sets of balanced phasors, namely positive sequence, negative sequence, and zero sequence.
The positive (or abc) sequence consists of three phasors of equal magnitude and separated from each other by an angle of 120°.
The negative (or cba) sequence also consists of three phasors of equal magnitude and separated from each other by an angle of 120°.
The zero sequence also consists of three phasors of equal magnitude, but they are all in phase.
These sequence components are illustrated in Figure 1.
The a phase is considered as the principal phase, and its sequence components are used to represent the other phases. Thus, the sequence components of phases b and c are given by Eqs. 1, 2, and 3.
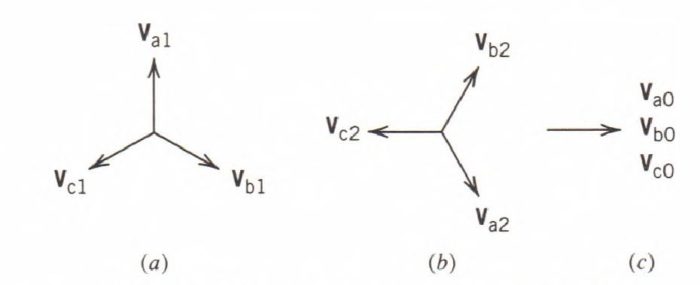
Figure 1: Sequence components of voltages.
$\begin{matrix} \begin{align} & {{V}_{b1}}={{V}_{a1}}{{e}^{j{{240}^{o}}}} \\ & {{V}_{c1}}={{V}_{a1}}{{e}^{j{{120}^{o}}}} \\\end{align} & {} & \left( 1 \right) \\\end{matrix}$
$\begin{matrix} \begin{align} & {{V}_{b2}}={{V}_{a2}}{{e}^{j{{120}^{o}}}} \\ & {{V}_{c2}}={{V}_{a2}}{{e}^{j{{240}^{o}}}} \\\end{align} & {} & \left( 2 \right) \\\end{matrix}$
$\begin{matrix} \begin{align} & {{V}_{b0}}={{V}_{a0}}{{e}^{j{{360}^{o}}}}={{V}_{a0}} \\ & {{V}_{c0}}={{V}_{a0}}{{e}^{j{{360}^{o}}}}={{V}_{a0}} \\\end{align} & {} & \left( 3 \right) \\\end{matrix}$
By introducing the operator $a={{e}^{j{{120}^{o}}}}=1\angle {{120}^{o}}$ , equations 1 and 2 may be written as:
$\begin{matrix} \begin{align} & {{V}_{b1}}={{a}^{2}}{{V}_{a1}} \\ & {{V}_{c1}}=a{{V}_{a1}} \\\end{align} & {} & \left( 4 \right) \\\end{matrix}$
$\begin{matrix} \begin{align} & {{V}_{b2}}=a{{V}_{a2}} \\ & {{V}_{c2}}={{a}^{2}}{{V}_{a2}} \\\end{align} & {} & \left( 5 \right) \\\end{matrix}$
The phase voltages are resolved into their sequence components and are expressed in terms of the sequence components of the principal phase a as follows:
\[\begin{matrix} {{V}_{a}}={{V}_{a0}}+{{V}_{a1}}+{{V}_{a2}} & {} & \left( 6 \right) \\\end{matrix}\]
\[\begin{matrix} \begin{align} & {{V}_{b}}={{V}_{b0}}+{{V}_{b1}}+{{V}_{b2}} \\ & ={{V}_{a0}}+{{a}^{2}}{{V}_{a1}}+a{{V}_{a2}} \\\end{align} & {} & \left( 7 \right) \\\end{matrix}\]
\[\begin{matrix} \begin{align} & {{V}_{c}}={{V}_{c0}}+{{V}_{c1}}+{{V}_{c2}} \\ & ={{V}_{a0}}+a{{V}_{a1}}+{{a}^{2}}{{V}_{a2}} \\\end{align} & {} & \left( 8 \right) \\\end{matrix}\]
In matrix form, Eqs. 6 to 8 may be expressed as
\[\begin{matrix} \left[ \begin{matrix} {{V}_{a}} \\ {{V}_{b}} \\ {{V}_{c}} \\\end{matrix} \right]=\left[ \begin{matrix} 1 & 1 & 1 \\ 1 & {{a}^{2}} & a \\ 1 & a & {{a}^{2}} \\\end{matrix} \right]\left[ \begin{matrix} {{V}_{a0}} \\ {{V}_{a1}} \\ {{V}_{a2}} \\\end{matrix} \right] & {} & \left( 9 \right) \\\end{matrix}\]
Adding Eqs. 6, 7, and 8 yields
$\begin{matrix} {{V}_{a}}+{{V}_{b}}+{{V}_{c}}=3{{V}_{a0}}+(1+{{a}^{2}}+a){{V}_{a1}}+(1+a+{{a}^{2}}){{V}_{a2}} & {} & \left( 10 \right) \\\end{matrix}$
The quantity inside the parentheses on the right-hand side of Eq. 10 may be shown to reduce to zero; that is,
$\begin{matrix} \begin{align} & 1+a+{{a}^{2}}=1+{{e}^{j120}}+{{e}^{j240}} \\ & =1\angle {{0}^{o}}+1\angle {{120}^{o}}+1\angle {{240}^{o}}=0+j0 \\\end{align} & {} & \left( 11 \right) \\\end{matrix}$
Therefore, the zero-sequence component of the voltage of the principal phase a is found as
$\begin{matrix} {{V}_{a0}}=\frac{1}{3}\left( {{V}_{a}}+{{V}_{b}}+{{V}_{c}} \right) & {} & \left( 12 \right) \\\end{matrix}$
Multiplying Eqs. 7 and 8 by the operators a and a2, respectively, and adding their products to Eq. 6 yields
$\begin{matrix} {{V}_{a}}+a{{V}_{b}}+{{a}^{2}}{{V}_{c}}=(1+a+{{a}^{2}}){{V}_{a0}}+3{{V}_{a1}}+(1+a+{{a}^{2}}){{V}_{a2}} & {} & \left( 13 \right) \\\end{matrix}$
By using Eq. 11, the positive-sequence component of the voltage is determined.
$\begin{matrix} {{V}_{a1}}=\frac{1}{3}\left( {{V}_{a}}+a{{V}_{b}}+{{a}^{2}}{{V}_{c}} \right) & {} & \left( 14 \right) \\\end{matrix}$
Similarly, Eqs. 7 and 8 may be multiplied by the operators a2 and a, respectively, and added to Eq. 6. Upon simplifying, the expression for the negative-sequence component of the voltage is obtained.
$\begin{matrix} {{V}_{a2}}=\frac{1}{3}\left( {{V}_{a}}+{{a}^{2}}{{V}_{b}}+a{{V}_{c}} \right) & {} & \left( 15 \right) \\\end{matrix}$
Equations 12, 14, and 15 may be grouped together and written in matrix form as follows:
\[\begin{matrix} \left[ \begin{matrix} {{V}_{a0}} \\ {{V}_{a1}} \\ {{V}_{a2}} \\\end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix} 1 & 1 & 1 \\ 1 & a & {{a}^{2}} \\ 1 & {{a}^{2}} & a \\\end{matrix} \right]\left[ \begin{matrix} {{V}_{a}} \\ {{V}_{b}} \\ {{V}_{c}} \\\end{matrix} \right] & {} & \left( 16 \right) \\\end{matrix}\]